什么是二面角
编辑二面角是两个相交的平面或半平面之间的角度。在化学中,它是通过两组三个原子的半平面之间的顺时针角度,有两个原子是共同的。在实体几何中,它被定义为一条线和两个以这条线为共同边缘的半平面的结合。在更高的维度上,二面角代表两个超平面之间的角度。当右舷和左舷的主平面(通常称为机翼)都向上倾斜于侧轴时,飞行器的平面被认为是正二面角。当向下倾斜时,它们被称为处于负二面角。
数学背景
编辑当两个相交的平面用直角坐标的两个方程式来描述时其中,nA-nB是矢量的点积,|nA||nB|是它们长度的积。在上述公式中需要绝对值,因为当改变一个方程中的所有系数符号,或用一个法向量替换其相反符号时,平面不会改变。然而,在考虑边界为同一直线的两个半平面的二面角时,可以而且应该避免使用绝对值。在这种情况下,半平面可以用它们的交点P和三个向量b0、b1和b2来描述,使P+b0、P+b1和P+b2分别属于交线、第一半平面和第二半平面。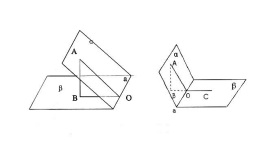
在高分子物理学中
编辑在一些科学领域,如高分子物理学,人们可以考虑一个点链和连续点之间的链接。如果这些点按顺序编号,并位于r1、r2、r3等位置,那么键向量的定义是u1=r2-r1,u2=r3-r2,ui=ri+1-ri,更普遍。蛋白质结构中的运动链或氨基酸就是这种情况。在这些情况下,人们往往对由三个连续点定义的半平面以及两个连续的这种半平面之间的二面角感兴趣。如果u1、u2和u3是三个连续的键向量,半平面的交点是有方向的,这就可以定义一个属于区间(-π,π)的二面角。
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/160798/
