精确覆盖

在数学领域的组合学中，给定一个集合X的子集的集合S，精确覆盖是S的一个子集S*，使得X中的每个元素都正好包含在S*的一个子集中。换句话说，S*是X的一个分区，由S中包含的子集组成。人们说，X中的每个元素正好被S*中的一个子集所覆盖。精确覆盖是一种覆盖。在计算机科学中，精确覆盖问题是一个决定性问题，以确定是否存在一个精确覆盖。精确覆盖问题是NP-完全的，是Karp的21个NP-完全问题之一。即使当S中的每个子集正好包含三个元素时，它也是NP-完全的；这个有限的问题被称为3集精确覆盖，通常缩写为X3C。精确覆盖问题是一种约束条件满足问题。一个精确覆盖问题可以用一个发生率矩阵或一个二方图来表示。Knuth的算法X是一种能找到精确覆盖问题的所有解决方案的算法。DLX是算法X的名称，当它在计算机上使用唐纳德-克努斯的DancingLinks技术有效实现时。标准的精确覆盖问题可以稍加概括，不仅涉及精确一的约束，而且涉及最多一的约束。

给定一个集合S的子集。的子集中的每个子集都至少包含一个元素。至少包含一个元素。

让S={N,O,P,E}是一个集合X={1,2,3,4}的子集的集合，这样。N={}，O={1，3}，P={1，2，3}，E={2，4}。子集{O，E}是X的精确覆盖，因为子集O={1，3}和E={2，4}是不相交的，它们的联合是X={1，2，3，4}。包括空集N={}也没有什么区别，因为它与所有的子集都不相交，不会改变并集。尽管子集E和P的联合是{1,2,3,4}=X，但子集E和P的交集{2}并不是空的。

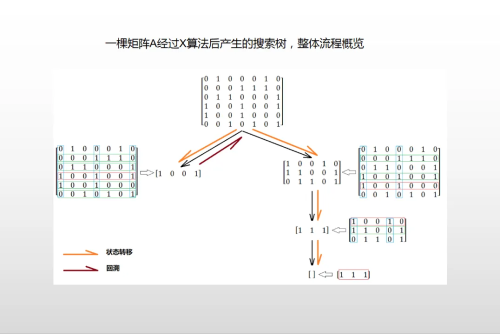
因此，子集E和P不符合完全覆盖的不相交要求。尽管N和P是不相交的，但它们的联合体不是X，所以它们不符合覆盖要求。另一方面，Y={1,2,3,4,5}也没有确切的覆盖--事实上，甚至没有一个覆盖，因为{displaystylebigcup{mathcal{S}}={1,2,3,4}}是Y的适当子集。是Y的一个适当的子集：S中没有一个子集包含元素5。

让S={A,B,C,D,E,F}是一个集合X={1,2,3,4,5,6,7}的子集的集合，这样。那么，子集S*={B，D，F}是一个精确覆盖，因为X中的每个元素都正好包含在其中一个子集中。此外，{B，D，F}是xxx的精确覆盖，正如下面的论证所表明的。因为A和B是xxx包含1的子集，一个完全覆盖必须包含A或B，但不能同时包含。