伯克霍夫算法（又称伯克霍夫-冯-诺伊曼算法）是一种将二元矩阵分解为包络矩阵的凸组合的算法。它有许多应用。其中一个应用是公平随机分配的问题：给定一个随机分配的项目，Birkhoff的算法可以将其分解为确定分配的抽签。

双随机矩阵（也称为：双随机）是一个矩阵，其中所有的元素都大于或等于0，每行和每列的元素之和等于1。

伯克霍夫算法的输入是一个双随机矩阵，输出则是伯克霍夫分解。

一个n乘n的矩阵X的置换集是X的n个条目的集合，正好包含每行和每列的一个条目。DénesKőnig的一个定理说。每一个双随机矩阵都有一个包络集，其中所有条目都是正的。一个n乘n的矩阵X的正性图是一个有2n个顶点的二方图，其中一边的顶点是n行，另一边的顶点是n列，如果某行和某列的条目是正的，则该行和该列之间有一条边。一个有正条目的互换集等同于正性图中的完美匹配。在二元图中的完美匹配可以在多项式时间内找到，例如，使用任何最大cardinality匹配的算法。Kőnig定理等同于以下内容。任何双线性矩阵的正性图都承认有完美匹配。如果一个矩阵的所有元素都是弱阳性，并且每一行和每一列的总和等于c，其中c是某个正常数，那么这个矩阵就被称为比例双态矩阵。换句话说，它是c乘以双痉挛矩阵。由于正性图不受缩放的影响。任何按比例排列的双随机矩阵的正演图都允许完美匹配。

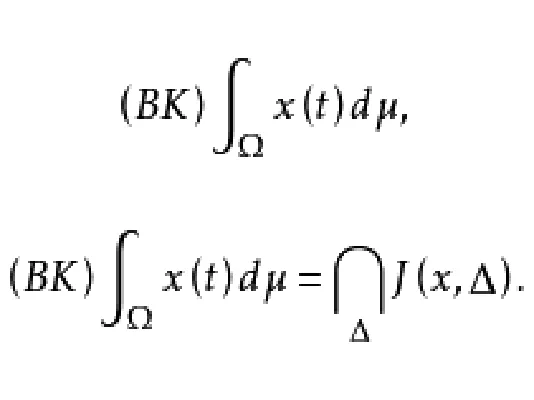
伯克霍夫算法是一种贪婪的算法：它贪婪地寻找完美匹配，并将其从分词匹配中删除。它的工作方式如下。

通过在步骤4中对z[i]的选择，在每个迭代中，X中至少有一个元素变成了0.因此，算法必须在最多n2步后结束。然而，最后一步必须同时使n个元素变成0，所以算法最多经过n2-n+1步就结束了。

在公平随机分配问题中，有n个对象和n个对对象有不同偏好的人。需要给每个人分配一个物品。为了实现公平，分配是随机的：对于每个（人，物）对，计算一个概率，使每个人和每个物的概率之和为1。概率序列程序可以计算概率，使每个代理人看着概率矩阵。