集合理论

集合理论是数理逻辑的一个分支，研究集合，可以非正式地描述为对象的集合。尽管任何类型的对象都可以被收集到一个集合中，但集合论作为数学的一个分支，主要关注那些与整个数学相关的对象。除了它的基础作用，集合论还提供了发展无穷大数学理论的框架，并在计算机科学（如关系代数理论）、哲学和形式语义学方面有各种应用。它的基础性吸引力，加上它的悖论、它对无穷大概念的影响以及它的多种应用，使集合论成为逻辑学家和数学哲学家的主要兴趣领域。

数学课题通常是通过许多研究者之间的相互作用而出现和发展的。然而，集合理论是由乔治-康托尔在1874年发表的一篇论文创立的。论所有实数代数的集合的一个属性。尤其值得注意的是19世纪上半叶伯纳德-博尔扎诺的工作。现代对无限的理解开始于1870-1874年，是由康托尔在实分析方面的工作推动的。康托尔的工作最初使他那个时代的数学家们产生了分歧。卡尔-魏尔斯特拉斯和戴德金支持康托，而现在被视为数学建构主义创始人的利奥波德-克朗纳克却不支持。由于康托尔概念的实用性，如集合之间的一一对应关系，他关于实数多于整数的证明，以及幂集运算产生的无穷大（康托尔的天堂），康托尔集合理论最终得到了广泛的应用。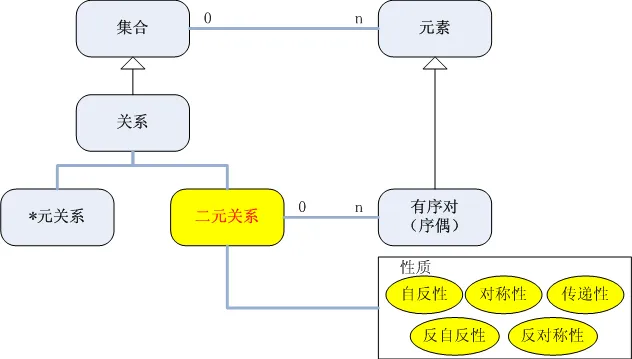

罗素没有使用"集合"一词，而是使用了"类"一词，这个词后来被用得更专业。分析家们的工作，如亨利-勒贝斯格的工作，证明了集合论的巨大数学效用，自此以后，集合论就被编织成了现代数学的结构。集合论通常被用作基础系统，尽管在某些领域--如代数几何和代数拓扑学--类别理论被认为是首选基础。

集合理论从一个对象o和一个集合A之间的基本二元关系开始，如果o是A的一个成员（或元素），则使用符号o∈A。