禁止图的表征

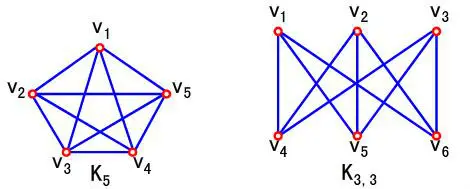
在图论这个数学分支中，许多重要的图族可以由不属于该图族的单个图的有限集合来描述，并进一步排除该图族中包含任何这些禁止图的（诱导）子图或小图的所有图。这种现象的一个典型例子是库拉托夫斯基定理，该定理指出，当且仅当一个图不包含两个禁图，即完整图K5和完整的二方图K3,3中的任何一个时，该图是平面的（可以在平面上没有交叉）。对于库拉托夫斯基定理，包含的概念是图的同构性，其中一个图的细分作为另一个图的子图出现。因此，每个图要么有一个平面图（在这种情况下，它属于平面图族），要么它至少有一个这两个图的细分作为子图。

更广泛地说，禁止图的特征是一种指定图族或超图结构的方法，通过指定禁止在该图族的任何图中存在的子结构。不同的家族在禁止的性质上有所不同。一般来说，一个结构G是一个家族的成员F的成员。当且仅当一个被禁止的子结构不包含在G中时，该被禁止的子结构可能是其中之一。子图，从大图的顶点和边的子集中得到的较小的图；诱导子图，通过选择顶点的一个子集并使用该子集中具有两个端点的所有边得到的较小的图；同构子图（也称为拓扑小图），通过将二级顶点的路径折叠成单边而从子图中得到的较小的图；或者图小图，通过任意的边收缩从子图中得到的较小的图。禁止属于某一图族的结构集也可以称为该图族的障碍集。禁止图的特征可用于测试一个图是否属于某一族的算法中。在许多情况下，有可能在多项式时间内测试一个给定的图是否包含障碍集的任何成员，因此它是否属于该障碍集所定义的族。为了使一个族具有禁止图的特征，并具有特定类型的子结构，该族必须在子结构下是封闭的。

也就是说，该族中一个图的每个子结构（特定类型）必须是该族中的另一个图。等价地，如果一个图不是家族的一部分，所有包含它作为子结构的更大的图也必须从家族中排除。当这一点为真时，总是存在一个阻碍集。然而，对于子结构的某些概念，这个障碍集可能是无限的。