混合图

在图论中，混合图G=（V，E，A）是由一组顶点V、一组（无定向）边E和一组定向边（或弧）A组成的图。

考虑相邻的顶点u,v∈V{displaystyleu,vinV}。.一条有向边，称为弧，是一条有方向的边，可以表示为uv→{displaystyle{overrightarrow{uv}}或｝或(u,v){displaystyle(u,v)}(注意u{displaystyleu}是尾巴。是尾巴，而v{displaystylev}是弧的头部。是弧的头部）。另外，一条无定向的边，或称边，是一条没有方向的边，可以表示为uv{displaystyleuv}或或[u,v].{displaystyle[u,v]}。.在我们的应用实例中，我们将不考虑混合图的循环或多条边。一个混合图中的行走是一个序列{displaystylev_{0},c_{1},v_{1},c_{2},v_{2},dots,c_{k},v_{k}}的顶点和边/弧，这样，对于所有的指数是图的一个弧。如果这个行走没有重复任何边、弧或顶点，可能除了xxx个和最后一个顶点之外，它就是一条路径。如果一条路径的xxx个和最后一个顶点是相同的，那么它就是封闭的；如果一条封闭的路径除了xxx个和最后一个顶点之外没有重复顶点，那么它就是一个循环。如果一个混合图不包含一个循环，那么它就是无循环的。着色混合图的着色可以被认为是对混合图的顶点进行标记或分配k种不同的颜色（其中k是一个正整数）。不同的颜色必须分配给由边连接的顶点。颜色可以用1到k的数字表示，对于一个有向弧，弧尾的颜色必须比弧头的数字小。我们可用来给混合图着色的k色是{1，2，3}。由于u和v由一条边连接，它们必须得到不同的颜色或标签（u和v分别被标为1和2）。

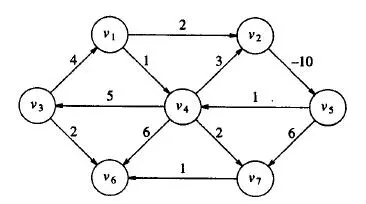
我们还有一条从v到w的弧。由于方位指定了一个顺序，我们必须给弧的尾部（v）贴上比弧的头部（w）更小的颜色（或我们集合中的整数）。在我们的弧上可以应用一个更弱的条件，我们可以认为一个混合图的弱的适当的k-coloring是一个函数c:V→[k]其中[k]:={1,2,...,k}，如果uv∈E，c(u)≠c(v)，如果c(u)≤c(v)存在性对于一个混合图来说，着色可能存在也可能不存在。为了使一个混合图有一个k着色，该图不能包含任何有向循环。如果这样的k染色存在，那么我们就把为图正确着色所需的最小k称为色度数，表示为χ(G)。我们可以将适当的k着色的数量计算为k的多项式函数，这被称为图G的色度多项式（与无定向图的色度多项式相类似），可以表示为χG(k)。计算弱色度多项式可以用删除-收缩法来计算混合图的弱色度多项式。这种方法包括删除（或移除）一条边或弧，并收缩（或连接）与该边（或弧）相关的其余顶点，以形成一个顶点。从混合图G=（V，E，A）中删除一条边e后，我们得到混合图（V，E-e，A）。同样，从一个混合图中删除一个弧，a，我们得到（V，E，A-a），我们可以把删除a的行为表示为G-a。根据上述命题，我们可以得到以下公式来计算混合图的色度多项式。

混合图可以用来模拟工作车间的调度问题，在这个问题中，要执行一系列的任务，并受到某些时间限制。在这种问题中，无向边可以用来模拟两个任务不兼容的约束（它们不能同时执行）。有向边可被用来建模，即两个任务是不相容的（不能同时执行）。