皮亚诺公理

在数理逻辑中，皮亚诺公理，也被称为戴德金-皮亚诺公理或皮亚诺公设，是19世纪意大利数学家朱塞佩-皮亚诺提出的自然数公理。这些公理在一些元数学研究中几乎没有改变过，包括对数论是否一致和完整的基本问题的研究。

直到赫尔曼-格拉斯曼（HermannGrassmann）的工作，人们才很好地认识到将算术形式化的必要性，他在19世纪60年代表明，算术中的许多事实可以从有关继承运算和归纳的更基本的事实中推导出来。

1881年，查尔斯-桑德斯-皮尔斯提供了一个自然数算术的公理化。1888年，理查德-戴德金提出了另一个自然数算术的公理化，1889年，皮亚诺在他的《用新方法介绍算术原理》（拉丁文：Arithmeticesprincipia,novamethodoexposita）一书中发表了这些公理的简化版本。

皮亚诺九条公理包含三种类型的陈述。xxx条公理断言自然数集合中至少有一个成员存在。接下来的四条是关于平等的一般陈述；在现代的处理中，这些常常不被视为佩阿诺公理的一部分，而是被视为基础逻辑的公理。

接下来的三个公理是关于自然数的一阶陈述，表达了继任运算的基本属性。第九条，也就是最后一条公理是关于自然数的数学归纳原则的二阶陈述，这使得这一表述接近于二阶算术。通过明确增加加法和乘法运算符号，并以一阶公理模式取代二阶归纳公理，就可以得到一个较弱的一阶系统，称为皮亚诺算术。

历史上的二阶表述当皮亚诺提出他的公理时，数理逻辑的语言正处于起步阶段。他为表述公理而创建的逻辑符号系统并没有被证明是流行的，尽管它是集合成员（∈，来自皮亚诺的ε）和隐含（⊃，来自皮亚诺的反转'C'）的现代符号的起源。

皮亚诺在数学和逻辑符号之间保持了明确的区分，这在数学中还不常见；这种区分最早是由戈特洛夫-弗雷格在1879年出版的《入门》中提出的。

皮亚诺不知道弗雷格的工作，他在布尔和施罗德的工作基础上独立地重新创建了他的逻辑装置。培诺公理定义了自然数的算术属性，通常表示为一个集合N或公理的非逻辑符号包括一个常数符号0和一个单项函数符号S。xxx条公理指出，常数0是一个自然数。

皮亚诺公理的最初表述是用1而不是0作为xxx个自然数，而Formulariomathematico中的公理则包括0。接下来的四条公理描述了平等关系。

由于它们在平等的一阶逻辑中逻辑上是有效的，因此在现代的处理中，它们不被认为是佩阿诺公理的一部分。对于每一个自然数x，x=x，即平等是反射性的。

对于所有自然数x和y，如果x=y，那么y=x，即平等是对称的。对于所有自然数x，y和z，如果x=y和y=z，那么x=z，即平等是传递性的。对于所有a和b，如果b是一个自然数，a=b，那么a也是一个自然数。

剩下的公理定义了自然数的算术属性。自然数被假定在单值继任函数S下是封闭的。

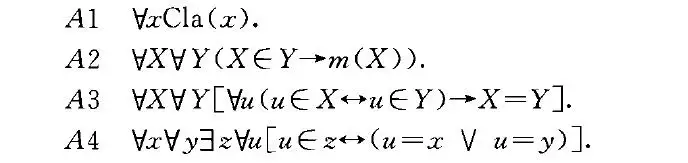
对于每个自然数n，S(n)是一个自然数。对于所有的自然数m和n，当且仅当S(m)=S(n)时，m=n，也就是说，自然数在S下是封闭的。对于每一个自然数n，S(n)=0是假的。

公理1、6、7、8定义了自然数的直观概念的单项表示：数字1可以定义为S(0)，2可以定义为S(S(0))，等等。

然而，考虑到自然数的概念是由这些公理定义的，公理1、6、7、8并不意味着继任函数产生了所有不同于0的自然数。

每一个自然数都可以通过对0足够频繁地应用继任函数而得到，这个直观的概念需要一个额外的公理，有时被称为归纳公理。如果K是一个集合，使得：0在K中，并且对于每个自然数n，n在K中意味着S(n)在K中，那么K包含每个自然数。归纳公理有时以下列形式表述。