简介
编辑Tseytin变换,也可以写成Tseitin变换,把一个任意的组合逻辑电路作为输入,产生一个共轭正常形式(CNF)的布尔公式,可以用CNF-SAT求解器来解决。
公式的长度与电路的大小呈线性关系。使电路输出为真的输入向量与满足该公式的赋值有1对1的对应关系。这就把任何电路(包括任何公式)上的电路可满足性问题简化为3-CNF公式的可满足性问题。
Tseytin变换的动机
编辑天真的方法是把电路写成布尔表达式,然后用DeMorgan定律和分布属性把它转换成CNF。然而,这可能会导致方程大小的指数级增长。Tseytin转换法输出的公式的大小相对于输入电路的大小是线性增长的。
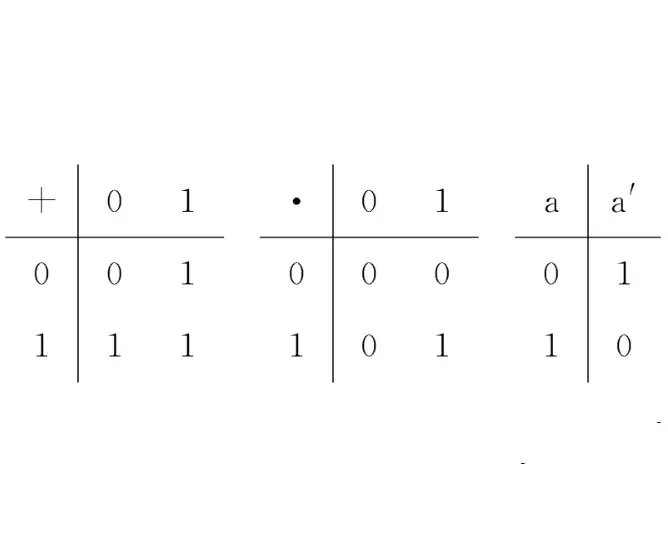
Tseytin变换的方法
编辑输出的方程是常数1设置为等于一个表达式。这个表达式是一个子表达式的组合,其中每个子表达式的满足都会使输入电路中的一个门正常工作。因此,整个输出表达式的满足就意味着整个输入电路的正常运行。
对于每一个门,都会引入一个代表其输出的新变量。一个预先计算好的与输入和输出相关的小型CNF表达式被附加到输出表达式上(通过AND操作)。
请注意,这些门的输入可以是原来的字词,也可以是代表子门输出的引入变量。尽管输出表达式比输入表达式包含更多的变量,但它仍然是可满足的,也就是说,当且仅当原始输入方程是可满足的,它才是可满足的。
当找到一个满意的变量赋值时,可以简单地丢弃那些引入变量的赋值。最后一个子句附加了一个字词:最后一个门的输出变量。如果这个字词是补足的,那么这个子句的满足将输出表达式强制为假;否则表达式将强制为真。
门的子表达式
编辑下面列出了一些可能的子表达式,可以为各种逻辑门创建。在操作表达式中,C作为一个输出;在CNF子表达式中,C作为一个新的布尔变量。对于每个操作,CNF子表达式是真的,当且仅当C在所有可能的输入值中遵守布尔操作的契约。
简单的组合逻辑
编辑下面的电路在至少有一些输入为真时返回真,但一次不能超过两个。它实现了方程式y=x1-x2+x1-x2+x2-x3。每个门的输出都引入了一个变量;这里每个都用红色标记。
请注意,以x2为输入的反相器的输出引入了两个变量。虽然这是多余的,但它并不影响所得方程的等价性。现在用适当的CNF子表达式替换每个门。
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/167809/
