非标准有限差分方案

非标准有限差分方案是数值分析中的一套通用方法，通过构建离散模型给出微分方程的数值解。这类方案的一般规则并不确切。

一个微分方程（DE）的有限差分（FD）模型可以通过简单地用FD近似值替换导数而形成。但这是一种天真的翻译。如果我们按字面意思将英语翻译成日语，在单词之间进行一对一的对应，往往就会失去原来的意义。同样地，一个DE的天真FD模型可能与原始DE非常不同，因为FD模型是一个差分方程，其解可能与DE的解大不相同。关于更多的技术定义，见Mickens2000。非标准（NS）有限差分模型，是微分方程的自由和更精确的翻译。例如，DE中的一个参数（称为v）在NS-FD模型中可能采取另一个值u。

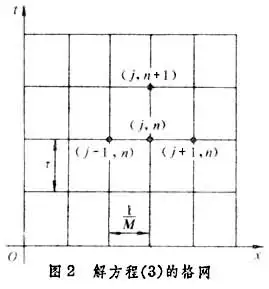
作为一个例子，让我们对波浪方程进行建模。天真的有限差分模型，也就是我们现在所说的标准（S）FD模型，是通过用FD近似值来求导数的。xxx导数的中心二阶FD近似为因为波浪方程的FD近似解与波浪方程本身并不相同。为了构建一个与波浪方程有相同解的NS-FD模型，可以用一个自由参数，称为u，来代替{displaystyle{left[{text{d}}_{t}{2}-(uDeltat/Deltax){2}{text{d}}_{x}{2}right]Psi(x,t)=0.}。进一步的细节和对二维和三维以及麦克斯韦方程的扩展可以在Cole2002中找到。