随机控制

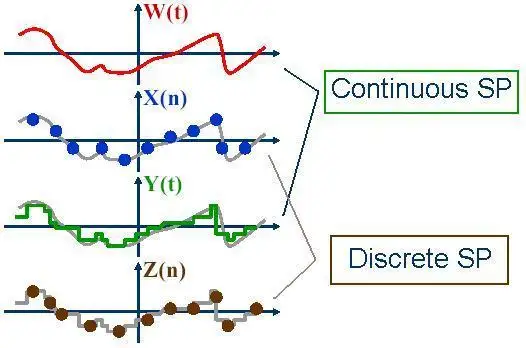
随机控制或随机最优控制是控制理论的一个子领域，它处理观察中或驱动系统演化的噪声中存在的不确定性。 系统设计者以贝叶斯概率驱动的方式假设，具有已知概率分布的随机噪声会影响状态变量的演化和观察。 随机控制旨在设计受控变量的时间路径，尽管存在这种噪声，但仍以最小的成本执行所需的控制任务，以某种方式定义。 上下文可以是离散时间或连续时间。

随机控制中一个研究得非常透彻的公式是线性二次高斯控制。 这里的模型是线性的，目标函数是二次型的期望值，扰动是纯加性的。 仅具有附加不确定性的离散时间集中系统的基本结果是确定性等价性质：在这种情况下的最优控制解决方案与在没有附加干扰的情况下获得的最优控制解决方案相同。 此属性适用于所有具有线性演化方程、二次成本函数和仅相加进入模型的噪声的集中式系统； 二次假设允许遵循确定性等价特性的最优控制法则是控制器观测值的线性函数。

与上述假设的任何偏差——非线性状态方程、非二次目标函数、模型乘法参数中的噪声或控制的分散——都会导致确定性等价性不成立。

在离散时间上下文中，决策者在每个时间段内观察状态变量，可能带有观察噪声。 目标可能是优化非线性（可能是二次）目标函数在从当前到最后一个关注时期的所有时间段内的期望值之和，或者仅优化目标函数的截至最后一个时期的值 . 在每个时间段进行新的观察，并对控制变量进行最佳调整。 找到当前时间的最优解可能涉及从上一期到当前期在时间上向后迭代矩阵 Riccati 方程。

在转移矩阵中参数值不确定的离散时间情况下（给出状态变量的当前值对其自身演化的影响）和/或状态方程的控制响应矩阵，但仍具有线性状态 方程和二次目标函数，即使确定性等价性不适用，仍然可以得到一个 Riccati 方程，用于向后迭代到每个周期的解。ch.13 非二次损失函数的离散时间情况，但只有加性扰动 也可以处理，尽管有更多的并发症。

离散时间随机线性二次控制问题的典型规范是最小化

其中E1为以y0为条件的期望值算子，上标T表示矩阵转置，S为时间范围，

其中 y 是一个 n × 1 的可观察状态变量向量，u 是一个 k × 1 的控制变量向量，At 是随机 n × n 状态转移矩阵的时间 t 实现，Bt 是随机 n × n 的时间 t 实现 k矩阵控制乘数，Q(n×n)和R(k×k)是已知的对称正定成本矩阵。 我们假设 A 和 B 的每个元素在时间上都是联合独立同分布的，因此期望值操作不需要是时间条件的。