条件熵
编辑在信息论中,条件熵量化描述随机变量 Y {dISPlaystyle Y} 的结果所需的信息量,前提是另一个随机变量 X {diSPlaystyle X} 的值已知。 在这里,信息以香农、纳特或哈特利来衡量。
定义
编辑给定 X {displaystyle X} 的 Y {displaystyle Y} 的条件熵定义为
(等式 1)
其中 X {displaystyle {mathcal {X}}} 和 Y {displaystyle {mathcal {Y}}} 表示 X {displaystyle X} 和 Y {displaystyle Y} 的支持集 .
注意:这里的约定是表达式 0 log 0 {displaystyle 0log 0} 应该被视为等于零。
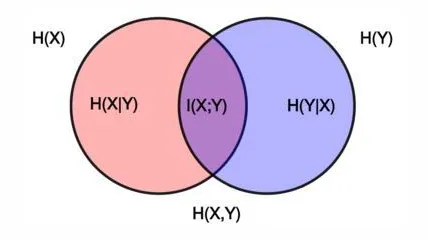
动机
编辑令 H ( Y | X = x ) {displaystyle mathrm {H} (Y|X=x)} 为以离散随机变量 X { 为条件的离散随机变量
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/193662/
