微分熵
编辑微分熵(也称为连续熵)是信息论中的一个概念,离散熵的实际连续版本是离散点的极限密度 (LDDP)。 微分熵(此处描述)在文献中很常见,但它是 LDDP 的极限情况,并且失去了与离散熵的基本联系。
在测度论方面,概率测度的微分熵是从该测度到勒贝格测度的负相对熵,后者被视为概率测度,尽管未归一化。
定义
编辑设 X {dISPlaystyle X} 是一个概率密度函数为 f {diSPlaystyle f} 的随机变量,它的支持是一个集合 X {displaystyle {mathcal {X}}} 。
对于没有显式密度函数表达式但具有显式分位数函数表达式的概率分布
与其离散模拟一样,微分熵的单位取决于对数的底数,通常为 2(即单位为位)。 不同底数的对数见对数单位。 联合、条件微分熵和相对熵等相关概念以类似的方式定义。 与离散模拟不同,微分熵有一个偏移量,该偏移量取决于用于测量 X {displaystyle X} 的单位。 例如,以毫米为单位测量的量的微分熵将比以米为单位测量的相同量多 log(1000); 无量纲量的微分熵 log(1000) 大于相同量除以 1000。
在尝试将离散熵的性质应用于微分熵时必须小心,因为概率密度函数可以大于 1。
请注意,连续互信息 I ( X ; Y ) {displaystyle I(X;Y)} 具有保留其作为离散信息度量的基本意义的区别,因为它实际上是分区的离散互信息的极限 X {displaystyle X} 和 Y {displaystyle Y} 随着这些分区变得越来越精细。 因此它在非线性同胚(连续且唯一可逆映射)下是不变的,包括 X {displaystyle X} 和 Y {displaystyle Y} 的线性变换,并且仍然表示可以传输的离散信息量 一个接纳连续价值空间的渠道。
对于扩展到连续空间的离散熵的直接模拟,请参见离散点的极限密度。
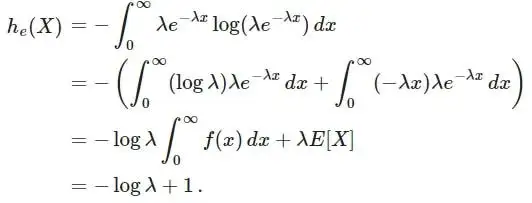
微分熵的性质
编辑- 对于概率密度 f {displaystyle f} 和 g {displaystyle g} ,Kullback–Leibler 散度 D K L ( f | | g ) {displaystyle D_{KL}(f||g)} 是 只有当 f = g {displaystyle f=g} 几乎所有地方都大于或等于 0 且相等。
- 微分熵的链式法则在离散情况下成立
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/193665/
