凯利公式
编辑在概率论中,凯利公式是一个确定下注最佳理论规模的公式。 当预期收益已知时,它是有效的。因为从长远来看,凯利标准比任何其他策略都带来更高的财富。
最佳投注示例
编辑使用凯利公式并根据实验中的赔率,正确的方法是在每次抛硬币时下注 20% 的资金,这 每轮平均收益为 2.034%。 这是几何平均数,不是算术率4% ( r = ( 1 + 0.2 ⋅ 1.0 ) 0.6 ⋅ ( 1 − 0.2 ⋅ 1.0 ) 0.4 {dISPlaystyle r=(1+0.2cdot 1.0){0.6 }cdot (1-0.2cdot 1.0){0.4}} )。 如果没有上限,300 轮后的理论预期财富为 $10,505 ( = 25 ⋅ ( 1.02034 ) 300 {diSPlaystyle =25cdot (1.02034){300}} )。
在这个特定的游戏中,由于上限的原因,在每次抛掷时仅下注底池的 12% 的策略会获得更好的结果(达到上限的概率为 95%,平均支出为 242.03 美元)。
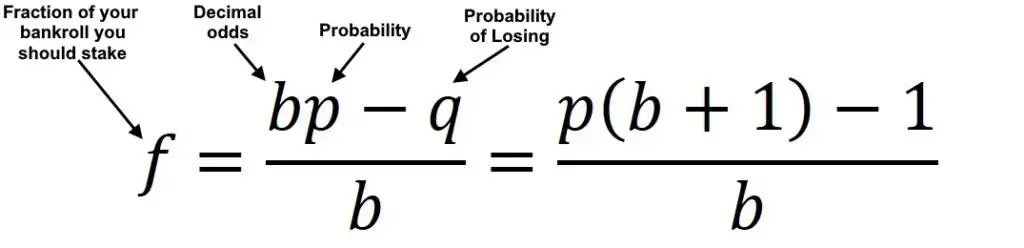
投资公式
编辑凯利公式的更一般形式允许部分损失,这与投资相关:
f ∗ = p a − q b {displaystyle f{*}={frac {p}{a}}-{frac {q}{b}}}
在哪里:
- f ∗ {displaystyle f{*}} 是应用于证券的资产部分。
- p {displaystyle p} 是投资增值的概率。
- q {displaystyle q} 是投资价值下降的概率 ( q = 1 − p {displaystyle q=1-p} )。
- a {displaystyle a} 是负数中丢失的分数
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/193687/
