集合论
编辑集合论是研究集合的数学逻辑的一个分支,集合可以非正式地描述为对象的集合。 虽然任何种类的对象都可以被收集到一个集合中,但集合论作为数学的一个分支,主要关注那些与整个数学相关的对象。
集合论的现代研究是由德国数学家理查德·戴德金和乔治·康托于 1870 年代发起的。 特别是,Georg Cantor 通常被认为是集合论的创始人。 在这个早期阶段研究的非形式化系统被称为朴素集理论。 在发现朴素集合论中的悖论(如罗素悖论、康托尔悖论和 Burali-Forti 悖论)后,20 世纪初提出了各种公理系统,其中 Zermelo-Fraenkel 集合论(与 或没有选择公理)仍然是最著名和研究最多的。
集合论通常被用作整个数学的基础系统,特别是以带有选择公理的 Zermelo-Fraenkel 集合论的形式出现。 除了其基础作用外,集合论还提供了发展无限数学理论的框架,并在计算机科学(例如关系代数理论)、哲学和形式语义学中有各种应用。 它的基本吸引力,连同它的悖论,它对无穷大概念的影响及其多重应用,使集合论成为逻辑学家和数学哲学家的主要兴趣领域。 当代对集合论的研究涵盖了广泛的主题,从实数轴的结构到大基数一致性的研究。
历史
编辑数学主题通常通过许多研究人员之间的互动而出现和发展。 然而,集合论是由 Georg Cantor 于 1874 年发表的一篇论文创立的:论所有实数代数数集合的性质。
自公元前 5 世纪以来,从西方的希腊数学家埃利亚的芝诺和东方的早期印度数学家开始,数学家们一直在与无穷大的概念作斗争。 尤其值得注意的是伯纳德·博尔扎诺 (Bernard Bolzano) 在 19 世纪上半叶的作品。 现代对无穷大的理解始于 1870 年至 1874 年,受到康托尔在实分析方面的工作的启发。 1872 年康托尔和理查德戴德金德之间的一次会面影响了康托尔的思想,并在康托尔 1874 年的论文中达到了顶峰。
康托尔的工作最初使他那个时代的数学家两极分化。 虽然 Karl Weierstrass 和 Dedekind 支持 Cantor,但现在被视为数学建构主义创始人的 Leopold Kronecker 却不支持。 由于康托尔概念的实用性,例如集合之间的一对一对应,他证明实数比整数多,以及无限中的无穷大(康托尔的天堂),康托尔集合论最终得到广泛传播 从电源组操作。 集合论的这种实用性导致了文章 Mengenlehre,该文章于 1898 年由 Arthur Schoenflies 贡献给克莱因的百科全书。
集合论的下一波热潮出现在 1900 年左右,当时人们发现康托尔集合论的某些解释引起了几个矛盾,称为二律背反或悖论。 BERTrAND Russell 和 Ernst Zermelo 独立发现了最简单和最著名的悖论,现在称为罗素悖论:考虑所有不是自身成员的集合,这导致矛盾,因为它必须是自身的成员而不是自身的成员 自己的一员。 1899年,康托尔自己提出了“所有集合的集合的基数是多少?”的问题,并得到了相关的悖论。 罗素在他 1903 年的《数学原理》中对大陆数学的评论中使用了他的悖论作为主题。 罗素没有使用术语集,而是使用了术语类,该术语后来在技术上得到了更多的使用。
集合论的势头如此之大,以至于关于悖论的辩论并没有导致它被放弃。 Zermelo 在 1908 年的工作以及 Abraham Fraenkel 和 Thoralf Skolem 在 1922 年的工作导致了公理集 ZFC,它成为集合论中最常用的公理集。 分析家的工作,例如亨利·勒贝格的工作,证明了集合论的巨大数学效用,此后它已融入现代数学的结构中。 集合论通常用作基础系统,尽管在某些领域(例如代数几何和代数拓扑)范畴理论被认为是首选基础。
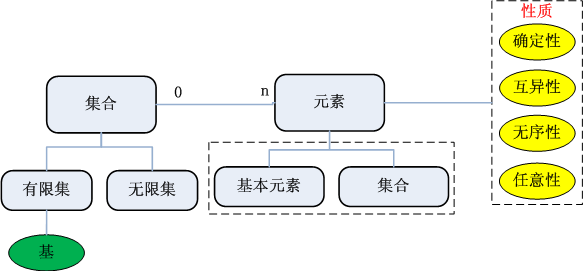
基本概念和符号
编辑集合论以对象 o 和集合 A 之间的基本二元关系开始。
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/198120/
