梯度下降法
编辑在数学中,梯度下降(通常也称为最速下降)是一种一阶迭代优化算法,用于寻找可微函数的局部最小值。 思路是在函数当前点的梯度(或近似梯度)的反方向重复走几步,因为这是最速下降的方向。 相反,沿梯度方向步进将导致该函数的局部最大值; 这个过程被称为梯度上升。
梯度下降法一般归因于奥古斯丁-路易斯柯西,他于1847年首先提出它。雅克阿达玛在1907年独立提出了类似的方法。它对非线性优化问题的收敛性质首先由Haskell Curry于1944年研究,用该方法 在接下来的几十年中得到越来越多的研究和使用。
描述
编辑可以保证收敛到局部最小值。 当函数 F {dISPlaystyle F} 是凸函数时,所有的局部最小值也是全局最小值,所以在这种情况下梯度下降可以收敛到全局解。
相邻图片说明了此过程。 这里假设 F {diSPlaystyle F} 定义在平面上,其图形呈碗状。 蓝色曲线是等高线,即 F {displaystyle F} 的值恒定的区域。 起源于一点的红色箭头表示该点负梯度的方向。 请注意,某个点的(负)梯度与通过该点的等高线正交。 我们看到梯度下降将我们引向碗底,即函数 F {displaystyle F} 的值最小的点。
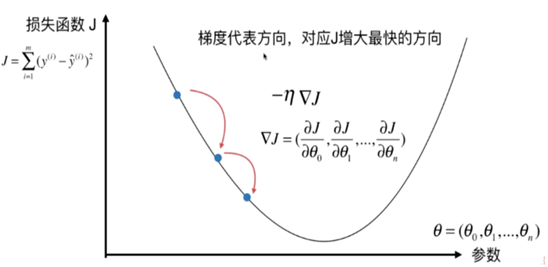
理解梯度下降的类比
编辑梯度下降背后的基本直觉可以通过一个假设场景来说明。 一个人被困在山上并试图下山(即试图找到全局最小值)。 雾很大,能见度极低。 因此,下山的路径是不可见的,所以他们必须利用本地信息来寻找最小值。 他们可以使用梯度下降法,即查看当前位置山坡的陡度,然后朝下降最陡的方向(即下坡)前进。
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/198155/
