拉格朗日乘数

在数学优化中，拉格朗日乘数 s 方法是一种寻找函数的局部xxx值和最小值的策略，该函数受等式约束（即，受一个或多个方程必须完全满足的条件的约束） 变量的选定值）。 它以数学家约瑟夫-路易斯·拉格朗日的名字命名。 基本思想是将约束问题转换为一种形式，使得仍然可以应用无约束问题的导数检验。 函数梯度和约束梯度之间的关系很自然地导致对原始问题的重新表述，称为拉格朗日函数。

并找到 L {\displaystyle {\mathcal {L}}} 的固定点，将其视为 x {\displaystyle x} 和拉格朗日乘数 λ {\displaystyle \lambda } 的函数； 这意味着所有偏导数都应该为零，包括关于 λ {\displaystyle \lambda } 的偏导数。 原始约束优化对应的解始终是拉格朗日函数的鞍点，可以根据带边海森矩阵的确定性在驻点中识别。

这种方法的xxx优点是它允许在不根据约束进行显式参数化的情况下解决优化问题。 因此，拉格朗日乘数的方法被广泛用于解决具有挑战性的约束优化问题。

以下被称为拉格朗日乘数定理。

拉格朗日乘数定理指出，在等式约束下计算的函数的任何局部xxx值（或最小值）处，如果约束条件适用（在下面解释），则函数的梯度（在该点）可以表示 作为约束梯度（在该点）的线性组合，拉格朗日乘数作为系数。 这相当于说任何垂直于约束的所有梯度的方向也垂直于函数的梯度。 或者仍然说函数的方向导数在每个可行方向上都为 0。

对于只有一个约束和两个选择变量的情况

（有时加法常量单独显示而不是包含在 g {\displaystyle g} 中，在这种情况下约束写为 g ( x , y ) = c {\displaystyle g(x,y)=c} ， 如图 1 所示。）我们假设 f {\displaystyle f} 和 g {\displaystyle g} 都具有连续的一阶偏导数。

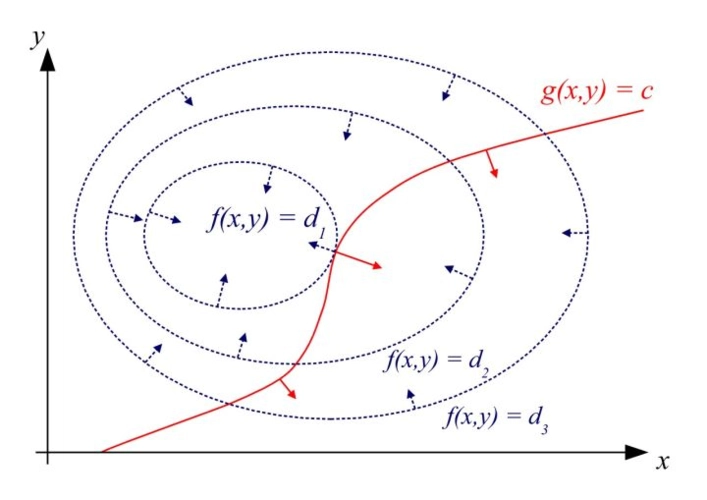
我们引入一个新变量 ( λ {\displaystyle \lambda } ) 称为拉格朗日乘数（或拉格朗日未定乘数）并研究由定义的拉格朗日函数（或拉格朗日或拉格朗日表达式）

其中可以添加或减去 λ {\displaystyle \lambda } 项。