精确覆盖问题
编辑在组合学的数学领域中,给定集合 X 的子集集合 S,精确覆盖是 S 的子集合 S*,使得 X 中的每个元素恰好包含在 S* 中的一个子集中。 换句话说,S* 是由 S 中包含的子集组成的 X 的划分。One 表示 X 中的每个元素恰好被 S* 中的一个子集覆盖。 精确覆盖是一种覆盖。
在计算机科学中,精确覆盖问题是判断是否存在精确覆盖的决策问题。 精确覆盖问题是 NP 完全问题,是 Karp 的 21 个 NP 完全问题之一。 即使 S 中的每个子集恰好包含三个元素,它也是 NP 完全的; 这个受限制的问题被称为 3 集的精确覆盖,通常缩写为 X3C。 精确覆盖问题是一种约束满足问题。
精确覆盖问题可以用关联矩阵或二分图表示。
Knuth 的算法 X 是一种找到精确覆盖问题的所有解决方案的算法。 DLX 是算法 X 在计算机上使用 Donald Knuth 的 Dancing Links 技术有效实施时的名称。
标准的精确覆盖问题可以稍微概括为不仅涉及恰好一个约束而且涉及至多一个约束。
寻找 Pentomino tilings 和解决 Sudoku 是精确覆盖问题的值得注意的例子。 n 皇后问题是一个稍微概括的精确覆盖问题。
正式定义
编辑给定集合 X {dISPlaystyle X} 子集的集合 S {diSPlaystyle S},X {displaystyle X} 的精确覆盖是 S 的子集合 S ∗ {displaystyle S{*}} {displaystyle S} 满足两个条件:
- S ∗ {displaystyle S{*}} 中任意两个不同子集的交集为空,即 S ∗ {displaystyle S{*}} 中的子集成对不相交。 换句话说,X {displaystyle X} 中的每个元素最多包含在 S ∗ {displaystyle S{*}} 中的一个子集中。
- S ∗ {displaystyle S{*}} 中子集的并集是 X {displaystyle X} ,即 S ∗ {displaystyle S{*}} 中的子集覆盖 X { 显示样式 X}。 换句话说,X {displaystyle X} 中的每个元素都包含在 S ∗ {displaystyle S{*}} 中的至少一个子集中。
简而言之,精确覆盖是指 X {displaystyle X} 中的每个元素恰好包含在 S ∗ {displaystyle S{*}} 中的一个子集中。
等价地,X {displaystyle X} 的精确覆盖是 S {displaystyle S} 的子集合 S ∗ {displaystyle S{*}} ,它划分了 X {displaystyle X} 。
要存在 X {displaystyle X} 的精确覆盖,必须:
- S {displaystyle S} 中子集的并集是 X {displaystyle X} 。 换句话说,X {displaystyle X} 中的每个元素都包含在 S {displaystyle S} 中的至少一个子集中。
如果空集 ∅ 包含在 S {displaystyle S} 中,那么它是否在任何精确覆盖中都没有区别。 因此,通常假设:
- 空集不在 S ∗ {displaystyle S{*}} 中。 换句话说,S ∗ {displaystyle S{*}} 中的每个子集至少包含一个元素。
基本示例
编辑设 S = {N, O, P, E} 是集合 X = {1, 2, 3, 4} 的子集的集合,使得:
- N = { },
- O = {1, 3},
- P = {1, 2, 3} 和
- E = {2, 4}。
子集合 {O, E} 是 X 的精确覆盖,因为子集 O = {1, 3} 和 E = {2, 4} 是不相交的,它们的并集是 X = {1, 2, 3, 4}。
子集合 {N, O, E} 也是 X 的精确覆盖。包括空集 N = { } 没有区别,因为它与所有子集都不相交并且不会改变并集。
子集合 {E, P} 不是 X 的精确覆盖。即使子集 E 和 P 的并集是 {1, 2, 3, 4} = X,子集 E 和 P 的交集,{2} , 不为空。 因此子集 E 和 P 不满足精确覆盖的不相交要求。
子集合 {N, P} 也不是 X 的精确覆盖。即使 N 和 P 不相交,但它们的并集不是 X,因此它们不符合覆盖要求。
另一方面,没有 Y = {1, 2, 3, 4, 5} 的精确覆盖——事实上,甚至没有覆盖——因为 ⋃ S = { 1 , 2 , 3 , 4 } {displaystyle bigcup {mathcal {S}}={1,2,3,4}} 是 Y 的真子集:S 中的子集都不包含元素 5。
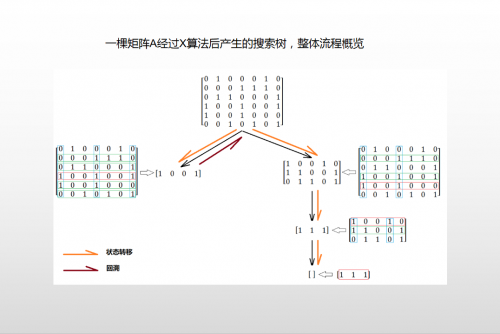
详细示例
编辑设 S = {A, B, C, D, E, F} 是集合 X = {1, 2, 3, 4, 5, 6, 7} 的子集的集合,使得:
- A = {1, 4, 7};
- B = {1, 4};
- C = {4, 5, 7};
- D = {3, 5, 6};
- E = {2, 3, 6, 7}; 和
- F = {2, 7}。
那么子集合 S* = {B, D, F} 是一个精确覆盖,因为 X 中的每个元素恰好包含在其中一个子集中:
- B = {1, 4};
- D = {3, 5, 6}; 或
- F = {2, 7}。
此外,{B, D, F} 是唯一的精确覆盖。
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/198203/
