幂等

等 (UK: /ˌɪdɛmˈpoʊtəns/, US: /ˈaɪdəm-/) 是数学和计算机科学中某些运算的属性，它们可以多次应用，而不改变初始应用后的结果。 幂等性的概念出现在抽象代数（特别是投影仪和闭包运算符的理论）和函数式编程（其中它与引用透明性相关联）的许多地方。

该术语由美国数学家本杰明皮尔士于 1870 年在代数元素的上下文中引入，这些元素在提升到正整数幂时保持不变，字面意思是（具有的质量）相同的权力，来自 idem + potential（相同 + 权力 ).

集合 S {displaystyle S} 的元素 x {displaystyle x} 配备二元运算符 ⋅ {displaystyle cdot } 在 ⋅ {displaystyle cdot } 下被认为是幂等的如果

x ⋅ x = x {displaystyle xcdot x=x} 。

二元运算 ⋅ {displaystyle cdot } 被认为是幂等的，如果

x ⋅ x = x {displaystyle xcdot x=x} 对于所有 x ∈ S {displaystyle xin S} 。

• 在具有乘法的自然数的幺半群 ( N , × ) {displaystyle (mathbb {N} ,times )} 中，只有 0 和 1 是幂等的。 实际上，0 × 0 = 0 {displaystyle 0times 0=0} 和 1 × 1 = 1 {displaystyle 1times 1=1}。
• 在加法自然数的幺半群 ( N , {displaystyle (mathbb {N} ,} +) 中，只有 0 是幂等的。事实上，0 + 0 = 0。
• 在岩浆 ( M , ⋅ ) {displaystyle (M,cdot )} 中，单位元素 e {displaystyle e} 或吸收元素 a {displaystyle a} ，如果它存在， 是幂等的。 事实上，e ⋅ e = e {displaystyle ecdot e=e} 和 a ⋅ a = a {displaystyle acdot a=a}。
• 在群 ( G , ⋅ ) {displaystyle (G,cdot )} 中，恒等元素 e {displaystyle e} 是xxx的幂等元素。 事实上，如果 x {displaystyle x} 是 G {displaystyle G} 的一个元素使得 x ⋅ x = x {displaystyle xcdot x=x} ，那么 x ⋅ x = x ⋅ e { displaystyle xcdot x=xcdot e} 最后 x = e {displaystyle x=e} 通过在左边乘以 x {displaystyle x} 的逆元素。
• 在幺半群 ( P ( E ) , ∪ ) {displaystyle ({mathcal {P}}(E),cup )} 和 ( P ( E ) , ∩ ) {displaystyle ( {mathcal {P}}(E),cap )} 幂集 P ( E ) {displaystyle {mathcal {P}}(E)} 集合 E {displaystyle E } 与集合并集 ∪ {displaystyle cup } 和集合交集 ∩ {displaystyle cap } 分别，∪ {displaystyle cup } 和 ∩ {displaystyle cap } 是幂等的。 事实上，x ∪ x = x {displaystyle xcup x=x} 对于所有 x ∈ P ( E ) {displaystyle xin {mathcal {P}}(E)} 和 x ∩ x = x {displaystyle xcap x=x} 对于所有 x ∈ P ( E ) {displaystyle xin {mathcal {P}}(E)} 。
• 在幺半群 ( { 0 , 1 } , ∨ ) {displaystyle ({0,1},vee )} 和 ( { 0 , 1 } , ∧ ) {displaystyle ( 布尔域的 {0,1},wedge )} 分别具有逻辑析取 ∨ {displaystyle vee } 和逻辑合取 ∧ {displaystyle wedge }， ∨ {displaystyle vee } 和 ∧ {displaystyle wedge } 是幂等的。 实际上，x ∨ x = x {displaystyle xvee x=x} 对于所有 x ∈ { 0 , 1 } {displaystyle xin {0,1}} 和 x ∧ x = x {displaystyle xwedge x=x} 对于所有 x ∈ { 0 , 1 } {displaystyle xin {0,1}} 。
• 在布尔环中，乘法是幂等的。
• 在热带半环中，加法是幂等的。
• 在二次矩阵环中，幂等矩阵的行列式为 0 或 1。如果行列式为 1，则矩阵必然为单位矩阵。

在幺半群 ( E E , ∘ ) {displaystyle (E{E},circ )} 中函数从集合 E {displaystyle E} 到自身（见集合取幂）与函数组合 ∘ { displaystyle circ } ，幂等元素是函数 f : E → E {displaystyle fcolon Eto E} 使得 f ∘ f = f {displaystyle fcirc f=f} ， 即 f ( f ( x ) ) = f ( x ) {displaystyle f(f(x))=f(x)} 对于所有 x ∈ E {displaystyle xin E} 换句话说，每个元素 x ∈ E {displaystyle xin E} 的图像 f ( x ) {displaystyle f(x)} 是 f {displaystyle f} ) 的不动点。 例如：

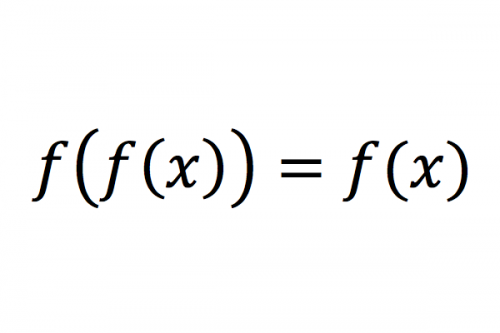
• xxx值是幂等的。 实际上，abs ∘ abs = abs {displaystyle operatorname {abs} circ operatorname {abs} =operatorname {abs} } ，即 abs ⁡ ( abs ⁡ ( x ) ) = abs ⁡ ( x ) {displaystyle operatorname {abs} (operatorname {abs} (x))=operatorname {abs} (x)} 对于所有 x {displaystyle x} ;
• 常量函数是幂等的；
• 身份函数是幂等的；
• 下限、上限和小数部分函数是幂等的；
• 群的幂集对自身的子群生成函数是幂等的；