命名微分方程列表ClassificationTypes

与流程的关系

• 差异（离散模拟）

• 随机指标
  • 随机偏
• 延迟

解决方案

存在性和唯一性

• 皮卡德–林德洛夫定理
• 皮亚诺存在性定理
• 卡拉西奥多里存在定理
• 柯西-科瓦列夫斯基定理

一般话题

• 初始条件
• 边界值
  • 狄利克雷
  • 纽曼
  • 罗宾
  • 柯西问题
• 朗斯基式
• 相貌
• 李雅普诺夫/渐近/指数稳定性
• 收敛速度
• 系列/整体解决方案
• 数值积分
• 狄拉克函数

解决方法

• 检查
• 特征方法
• 欧拉
• 指数响应公式
• 有限差分（Crank–Nicolson）
• 有限元
  • 无限元
• 有限体积
• 伽辽金
  • 彼得罗夫-伽辽金

无限元法是一种解决工程和数学物理问题的数值方法。

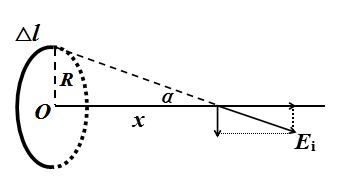
它是有限元法的一种改进。 该方法将有关域划分为无限长的部分。 与通过有限支持上的多项式表达式逼近的有限元相比，无限元的无界长度装有允许在渐近线处评估场的函数。 函数和插值点的数量定义了元素在无限方向上的精度。 该方法通常用于解决声学问题，并允许遵守声波不返回和压力波在远场扩散的 Sommerfeld 条件。