费根鲍姆常数
编辑在数学中，特别是分岔理论中，费根鲍姆常数是两个数学常数，它们都表示非线性映射分岔图中的比率。
历史
编辑Feigenbaum 最初将xxx个常数与 logistic 映射中的倍周期分岔联系起来，但也表明它适用于所有具有单个二次xxx值的一维映射。 由于这种普遍性，与这种描述相对应的每个混沌系统都将以相同的速率分叉。
xxx个常量
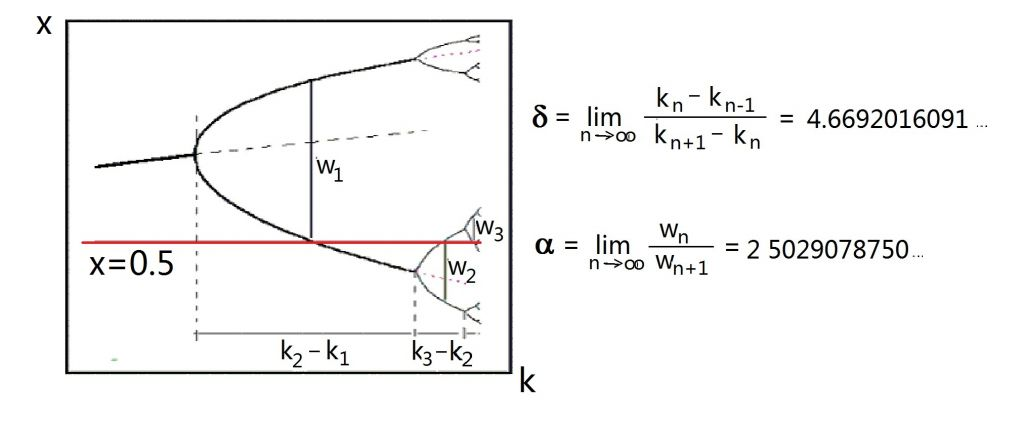
编辑xxx个 Feigenbaum 常数 δ 是单参数映射的每个周期加倍之间每个分叉间隔与下一个分叉间隔的限制比
其中 f(x) 是由分岔参数 a 参数化的函数。
价值
- 30 位小数：δ = 4.669201609102990671853203820466 ...
- （OEIS 中的序列 A006890）
- 一个简单的有理近似值是：621/133，它对 5 个有效值（四舍五入时）是正确的。 要获得更高的精度，请使用 1228/263，它对 7 个有效值是正确的。
- 约等于10(1/π − 1)，误差为0.0015%
插图
非线性映射
这里a是分岔参数，x是变量。 周期加倍的 a 的值（例如没有周期 2 轨道的 a 的xxx值，或没有周期 4 轨道的xxx a）是 a1、a2 等。这些列于下表：
最后一列中的比率收敛于xxx个 Feigenbaum 常数。 逻辑地图出现相同的数字
具有实参 a 和变量 x。 再次列出分叉值：
分形
分岔参数是周期为 2n 分量的根点。 该级数收敛于费根鲍姆点 c = −1.401155…… 最后一列中的比率收敛于xxx个费根鲍姆常数。
其他地图也复制了这个比率，在这个意义上，分岔理论中的 Feigenbaum 常数类似于几何学中的 π 和微积分中的 e。
第二个常量
编辑第二个 Feigenbaum 常数或 Feigenbaum 的 alpha 常数（OEIS 中的序列 A006891），
是齿的宽度与其两个子齿之一的宽度之间的比率（除了最靠近折叠的齿）。 当测量下部尖齿与尖齿宽度之间的比率时，将负号应用于 α。
属性
编辑这两个数字都被认为是超越的，尽管它们还没有被证明是这样。 也没有已知的证据表明这两个常数都是无理数。
内容由匿名用户提供，本内容不代表vibaike.com立场，内容投诉举报请联系vibaike.com客服。如若转载，请注明出处：https://vibaike.com/214439/