迭代函数

在数学中，迭代函数是函数 X → X（即从某个集合 X 到自身的函数），它是通过将另一个函数 f : X → X 与自身组合一定次数而获得的。 重复应用相同函数的过程称为迭代。 在此过程中，从某个初始对象开始，应用给定函数的结果再次作为输入馈入函数，并重复此过程。

代函数是计算机科学、分形、动力系统、数学和重整化群物理学的研究对象。

集合 X 上迭代函数的正式定义如下。

设 X 是一个集合，f: X → X 是一个函数。

将 f n 定义为 f 的第 n 次迭代（由 Hans Heinrich Bürmann 和 John Frederick William Herschel 引入的符号），其中 n 是一个非负整数，通过： f 0 = d e f id X {displaystyle f{0} ~{stackrel {mathrm {def} }{=}}~operatorname {id} _{X}} 和 f n + 1 = d e f f ∘ f n , {displaystyle f{n+1}~ {stackrel {mathrm {def} }{=}}~fcirc f{n},}

其中 idX 是 X 上的恒等函数，f○g 表示函数组合。 那是，

(f○g)(x) = f (g(x)),

总是联想的。

因为符号 f n 可能指代函数 f 的迭代（复合）或函数 f 的求幂（后者常用于三角学），一些数学家选择使用 ∘ 来表示复合意义，写作 f∘n(x ) 对于函数 f(x) 的第 n 次迭代，例如，f∘3(x) 表示 f(f(f(x)))。 出于同样的目的，Benjamin Peirce 使用 f [n](x)，而 Alfred Pringsheim 和 Jules Molk 建议改用 nf(x)。

通常，以下恒等式适用于所有非负整数 m 和 n，

f m ∘ f n = f n ∘ f m = f m + n 。 {displaystyle f{m}circ f{n}=f{n}circ f{m}=f{m+n}~.}

这在结构上等同于求幂的性质 aman = am + n，即特殊情况 f(x) = ax。

一般来说，对于任意一般（负数、非整数等）指数 m 和 n，这种关系称为平移函数方程，参见。 施罗德方程和阿贝尔方程。 在对数标度上，这归结为切比雪夫多项式的嵌套属性 Tm(Tn(x)) = Tm n(x)，因为 Tn(x) = cos(n arccos(x))。

关系 (f m)n(x) = (f n)m(x) = f mn(x) 也成立，类似于指数的性质 (am)n = (an)m = amn。

函数序列 f n 称为 Picard 序列，以 Charles Émile Picard 的名字命名。

对于 X 中的给定 x，值序列 fn(x) 称为 x 的轨道。

如果 f n (x) = f n+m (x) 对于某个整数 m，则该轨道称为周期轨道。 对于给定的 x，最小的 m 值称为轨道周期。 点 x 本身称为周期点。 计算机科学中的周期检测问题是寻找轨道中xxx个周期点和轨道周期的算法问题。

如果f(x) = x 对于X 中的某个x（即x 的轨道周期为1），则称x 为迭代序列的不动点。 不动点集通常表示为 Fix(f)。 有许多不动点定理保证不动点在各种情况下的存在，包括Banach不动点定理和Brouwer不动点定理。

有几种技术可以加速不动点迭代产生的序列的收敛。 例如，应用于迭代不动点的 Aitken 方法称为 Steffensen 方法，并产生二次收敛。

迭代后，人们可能会发现有些集合会收缩并收敛到一个点。 在这种情况下，收敛到的点称为吸引不动点。 相反，迭代可能会出现从单个点发散的点； 对于不稳定的固定点，情况就是如此。 当轨道上的点收敛到一个或多个极限时，轨道上的累积点集称为极限集或ω-极限集。

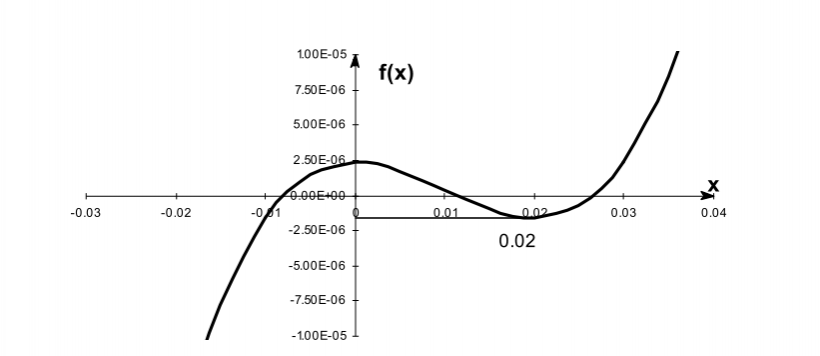
吸引和排斥的概念具有相似的概括性； 根据迭代下小邻域的行为，可以将迭代分为稳定集和不稳定集。 （另见解析函数的无限组合。）

其他限制行为也是可能的； 例如，漫游点是移动的点，即使靠近它们的起点也永远不会回来。

如果考虑密度分布的演变，而不是单个点动力学的演变。