晶体学点群
编辑在晶体学中,晶体学点群是一组对称操作,对应于三个维度中的一个点群,这样每个操作(可能之后是平移)都会使晶体的结构保持不变,即相同种类的原子 将被放置在与改造前相似的位置。 例如,在立方晶系的许多晶体中,晶胞绕垂直于立方体其中一个面的轴旋转 90 度是一种对称操作,它将每个原子移动到另一个原子的位置 同类,不影响晶体的整体结构。
在晶体分类中,每个点群定义一个所谓的(几何)晶体类。 三维点群有无穷多个。 然而,晶体学对一般点群的限制导致只有 32 个晶体学点群。
晶体的点群决定了由其结构引起的物理特性的方向变化,包括双折射等光学特性或普克尔斯效应等电光特性。 对于周期性晶体(与准晶体相反),该群必须保持定义结晶度的三维平移对称性。
符号
编辑点群根据它们的分量对称性命名。 晶体学家、矿物学家和物理学家使用了几种标准符号。
Schoenflies 符号
编辑在 Schoenflies 表示法中,点群由带下标的字母符号表示。
由于晶体限制定理,在 2 维或 3 维空间中 n = 1、2、3、4 或 6。
D4d 和 D6d 实际上是被禁止的,因为它们分别包含 n=8 和 12 的不当旋转。 表中的27个点群加上T、Td、Th、O、Oh构成了32个晶体学点群。
Hermann–Mauguin 表示法
编辑通常用于空间群的 Hermann-Mauguin 符号的缩写形式也用于描述晶体学点群。
不同符号之间的对应关系
编辑同构
编辑许多晶体点群共享相同的内部结构。 例如,点群 1、2 和 m 包含不同的几何对称操作(分别为反转、旋转和反射),但都共享循环群 C2 的结构。 所有同构群都是同阶的,但并非所有同阶群都是同构的。 同构的点群如下表所示:
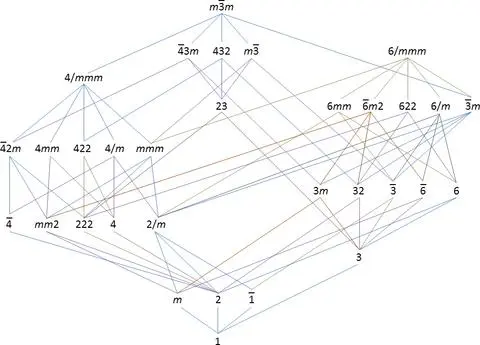
此表使用循环组(C1、C2、C3、C4、C6)、二面体组(D2、D3、D4、D6)、交替组之一(A4)和对称组之一(S4)。 这里符号×表示直积。
从空间群导出晶体学点群(晶体类)
编辑- 省略 Bravais 晶格类型。
- 将所有具有平移分量的对称元素转换为各自不具有平移对称性的对称元素。 (滑动平面转换为简单的镜像平面;螺旋轴转换为简单的旋转轴。)
- 旋转轴、旋转反转轴和镜像平面保持不变。
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/214833/
