最密堆积
编辑在几何学中,球体堆积是在包含空间内的非重叠球体的排列。 所考虑的球体通常都是相同大小的,空间通常是三维欧氏空间。 然而,球体填充问题可以推广到考虑不等球体、其他维度的空间(其中问题变成二维的圆形填充,或更高维度的超球体填充)或非欧几里得空间,如双曲空间。
一个典型的球体填充问题是找到一种排列方式,使球体尽可能多地填充空间。 球体填充的空间比例称为排列的堆积密度。 由于无限空间中填料的局部密度会根据测量体积而变化,因此问题通常是在足够大的体积上测量的平均密度或渐近密度最大化。
对于三个维度上的相等球体,最密集的堆积使用大约 74% 的体积。 等球体的随机堆积通常具有大约 63.5% 的密度。
分类和术语
编辑晶格排列(通常称为规则排列)是其中球体的中心形成非常对称的图案,只需要唯一定义 n 个向量(在 n 维欧几里德空间中)。 晶格排列是周期性的。 球体不形成晶格(通常称为不规则)的排列仍然可以是周期性的,但也可以是非周期性的(正确地说是非周期性的)或随机的。 由于它们的高度对称性,晶格填料比非晶格填料更容易分类。 周期性晶格总是具有明确定义的密度。
常规包装
编辑密集包装
编辑在三维欧几里德空间中,等球体的最密集堆积是由称为密堆积结构的结构族实现的。 生成这种结构的一种方法如下。 考虑一个平面,上面有紧凑排列的球体。 称它为 A。对于任何三个相邻的球体,第四个球体可以放在三个底部球体之间的空心顶部。 如果我们对第一个平面上方的第二个平面中的一半孔执行此操作,我们将创建一个新的致密层。 这样做有两种可能的选择,称它们为 B 和 C。假设我们选择 B。那么 B 的一半空心位于 A 中球的中心上方,另一半位于 A 的空心上方,而 A 的空心不是 用于 B。因此,第三层的球可以直接放置在第一层的球上方,从而产生 A 型层,或者可以放置在第一层未被第二层占据的孔上方,从而产生 A C 型层。组合 A、B 和 C 型层产生各种密堆积结构。
密排族中的两个简单排列对应于规则格。 一种称为立方密堆积(或面心立方,FCC)——其中各层按 ABCABC… 顺序交替排列。 另一种称为六角密堆积 (HCP),其中各层按 ABAB… 顺序交替排列。 但许多层堆叠序列是可能的(Abac、ABCBA、ABCBAC 等),并且仍然生成密排结构。 在所有这些排列中,每个球体接触 12 个相邻的球体,平均密度为
π 3 2 ≃ 0.74048。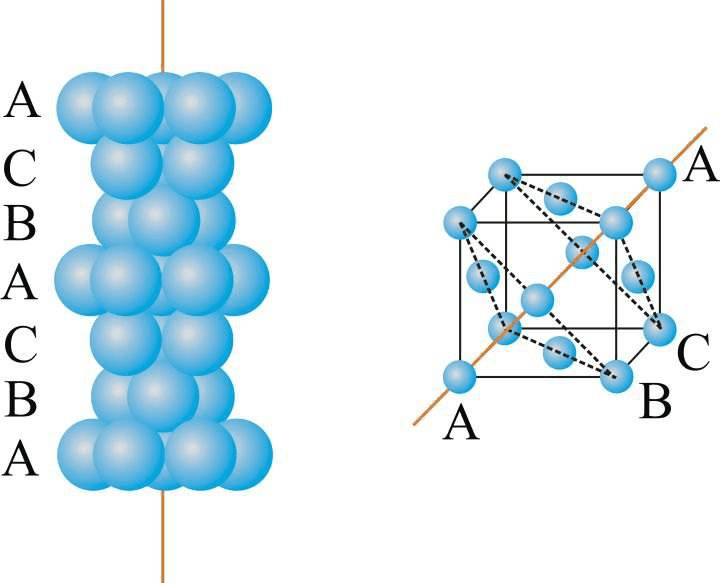
其他常见的点阵填料
编辑在物理系统中经常会发现其他一些晶格堆积。 其中包括密度为 π 6 ≈ 0.5236的立方晶格,密度为 π 3 3 ≈ 0.6046 和密度为 π 3 16 ≈ 0.3401,并且在 0.0555 的密度下可能最松散。
低密度堵塞填料
编辑所有球体都被其相邻球体限制在一个位置的填充称为刚性或堵塞。 密度最低的严格堵塞的球体堆积是密度仅为 0 的稀释(隧道状)面心立方晶体。
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/214887/
