阿伦尼乌斯方程

在物理化学中，阿伦尼乌斯方程是反应速率的温度依赖性公式。 该方程由 Svante Arrhenius 于 1889 年根据荷兰化学家 Jacobus Henricus van 't Hoff 的工作提出，他在 1884 年注意到平衡常数对温度依赖性的 van 't Hoff 方程暗示了这样一个公式 正向和反向反应的速率。 该方程在确定化学反应速率和计算活化能方面具有广泛而重要的应用。 Arrhenius 为该公式提供了物理依据和解释。 目前，xxx将其视为经验关系。 它可用于模拟扩散系数的温度变化、晶体空位的数量、蠕变速率和许多其他热诱导过程/反应。 1935年发展起来的艾林方程也表达了速率和能量之间的关系。

阿伦尼乌斯方程序给出了化学反应的速率常数对xxx温度的依赖性 k = A e − E a R T , {\displaystyle k=Ae{\frac {-E_{\rm {a}}}{RT}},} 其中

• k 是速率常数（导致反应的碰撞频率），
• T 是xxx温度（以开尔文或朗肯度为单位），
• A 是指前因子。 Arrhenius 最初认为 A 是每个化学反应的与温度无关的常数。 然而，最近的治疗包括一些温度依赖性 - 请参阅下面的改良阿伦尼乌斯方法。
• Ea 是反应的活化能（单位与 RT 相同），
• R 是通用气体常数。

或者，方程可以表示为 k = A e − E a k B T , {\displaystyle k=Ae{\frac {-E_{\rm {a}}}{k_{\rm {B}} T}},} 其中

• Ea 是反应的活化能（单位与 kBT 相同），
• kB 是玻尔兹曼常数。

xxx不同的是 Ea 的能量单位：前者使用化学中常见的每摩尔能量，而后者直接使用物理中常见的每分子能量。 气体常数 R 或玻尔兹曼常数 kB，作为温度 T 的乘数。

指前因子 A 的单位与速率常数的单位相同，并且会根据反应的顺序而变化。 如果反应是一阶反应，它的单位是：s−1，因此它通常被称为频率因子或反应的尝试频率。 最简单的是，k 是每秒导致反应的碰撞次数，A 是每秒以正确的反应方向发生的碰撞（导致或不导致反应）的次数，e − E a / ( R T ) { \displaystyle e{-E_{\rm {a}}/(RT)}} 是任何给定碰撞将导致反应的概率。 可以看出，提高温度或降低活化能（例如通过使用催化剂）将导致反应速率增加。

鉴于动力学研究的小温度范围，将活化能近似视为与温度无关是合理的。 同样，在广泛的实际条件下，与 exp ⁡ ( − E a / ( R T ) ) {\displaystyle \exp(-E_ {\rm {a}}/(RT))} 因子； 除了在无障碍扩散限制反应的情况下，在这种情况下，指前因子占主导地位并且可以直接观察到。

通过这个等式，可以粗略地估计温度每升高 10°C，反应速率会增加约 2 或 3 倍。

e − E a R T {\displaystyle e{\frac {-E_{a}}{RT}}} 表示能量大于或等于 E a {\displaystyle E_{a} } 。

取阿伦尼乌斯方程的自然对数得到： ln ⁡ k = ln ⁡ A − E a R 1 T 。 {\displaystyle \ln k=\ln A-{\frac {E_{\rm {a}}}{R}}{\frac {1}{T}}。}

重新排列收益率：ln ⁡ k = − E a R ( 1 T ) + ln ⁡ A 。 {\displaystyle \ln k={\frac {-E_{\rm {a}}}{R}}\left({\frac {1}{T}}\right)+ ln A.}

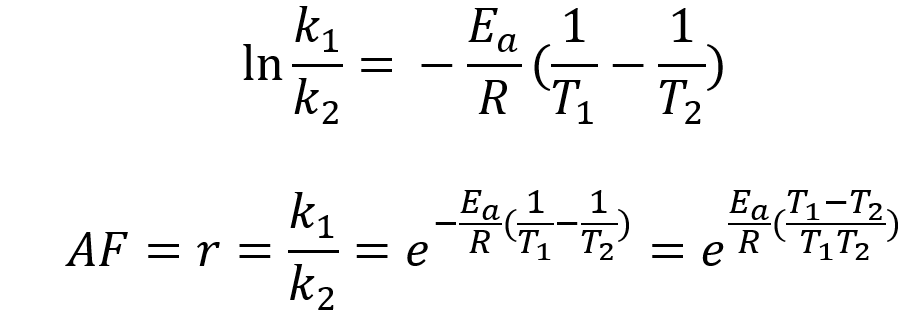
这与直线方程的形式相同： y = m x + c , {\displaystyle y=mx+c,}

其中 x 是 T 的倒数。

因此，当反应的速率常数服从阿伦尼乌斯方程时，ln k 与 T−1 的关系图给出一条直线，其梯度和截距可用于确定 Ea 和 A。 这个过程在实验化学动力学中变得如此普遍，以至于从业者已经开始使用它来定义反应的活化能。 也就是说，活化能定义为 (−R) 乘以 ln k 与 (1/T) 曲线的斜率：E a ≡ − R [ ∂ ln ⁡ k ∂ ( 1 / T ) ] P 。