理想气体状态方程

系统属性注意：共轭变量以斜体显示

材料特性

• 属性数据库

可压缩性 β = − {displaystyle beta =-}
热膨胀 α = {displaystyle alpha =}

方程式

• 卡诺定理
• 克劳修斯定理
• 基本关系
• 理想气体状态过程

• 麦克斯韦关系
• Onsager 互惠关系
• 布里奇曼方程
• 热力学方程表

潜力

• 自由能
• 自由熵

• 内能 U ( S , V ) {displaystyle U(S,V)}
• 焓 H ( S , p ) = U + p V {displaystyle H(S,p)=U+pV}
• 亥姆霍兹自由能 A ( T , V ) = U − T S {displaystyle A(T,V)=U-TS}
• 吉布斯自由能 G ( T , p ) = H − T S {displaystyle G(T,p)=H-TS}

• 历史
• 文化

科学家们

• 伯努利
• 玻尔兹曼
• 布里奇曼
• 卡拉西奥多里
• 卡诺
• 克拉佩龙
• 克劳修斯
• 德唐德
• 迪昂
• 吉布斯
• 冯·亥姆霍兹
• 焦耳
• 刘易斯
• 马修
• 麦克斯韦
• 冯迈耶
• 能斯特
• 昂萨格
• 普朗克
• 兰金
• 史密顿
• 斯塔尔
• 泰特
• 汤普森
• 汤姆逊
• 范德瓦尔斯
• 沃特斯顿

其他

• 成核
• 自组装
• 自组织
• 秩序与混乱

理想气体定律，也称为一般气体方程，是一种假设的理想气体的状态方程。 它是许多气体在许多条件下行为的良好近似，尽管它有一些局限性。 它由 Benoît Paul Émile Clapeyron 于 1834 年首次提出，它是经验波义耳定律、查尔斯定律、阿伏伽德罗定律和盖-吕萨克定律的组合。 理想气体定律通常以经验形式书写：

p V = n R T {displaystyle pV=nRT} 其中 p {displaystyle p} , V {displaystyle V} 和 T {displaystyle T} 是压力、体积和温度； n {displaystyle n} 是物质的数量； 并且 R {displaystyle R} 是理想气体常数。它也可以从微观动力学理论推导出来，正如奥古斯特·克伦尼希 (August Krönig) 于 1856 年和鲁道夫·克劳修斯 (Rudolf Clausius) 于 1857 年所取得的（显然是独立地）。

一定量气体的状态由其压力、体积和温度决定。 等式的现代形式将这些简单地以两种主要形式联系起来。 状态方程中使用的温度是绝对温度：合适的 SI 单位是开尔文。

最常引入的形式是： p V = n R T = n k B N A T = N k B T {displaystyle pV=nRT=nk_{text{B}}N_{text{A}}T=Nk_{ text{B}}T} 其中：

• p {displaystyle p} 是气体的xxx压力，
• V {displaystyle V} 是气体的体积，
• n {displaystyle n} 是气体物质的量（也称为摩尔数），
• R {displaystyle R} 是理想的或通用的气体常数，等于玻尔兹曼常数和阿伏加德罗常数的乘积，
• k B {displaystyle k_{text{B}}} 是玻尔兹曼常数，
• N A {displaystyle N_{A}} 是阿伏加德罗常数，
• T {displaystyle T} 是气体的xxx温度，
• N {displaystyle N} 是气体粒子（通常是原子或分子）的数量。

在 SI 单位中，p 的单位是帕斯卡，V 的单位是立方米，n 的单位是摩尔，T 的单位是开尔文（开尔文温标是一种移动的摄氏温标，其中 0.00 K = −273.15 °C，可能的最低温度 ). R 的值为 8.314 J/(mol·K) = 1.989 ≈ 2 cal/(mol·K)，或 0.0821 L·atm/(mol·K)。

可以通过给出质量而不是气体的化学量来指定存在多少气体。 因此，理想气体定律的另一种形式可能会有用。 化学量 n（以摩尔为单位）等于气体的总质量 (m)（以千克为单位）除以摩尔质量 M（以千克/摩尔为单位）：

n = m M 。 {displaystyle n={frac {m}{M}}。}

通过用 m/M 替换 n 并随后引入密度 ρ = m/V，我们得到：

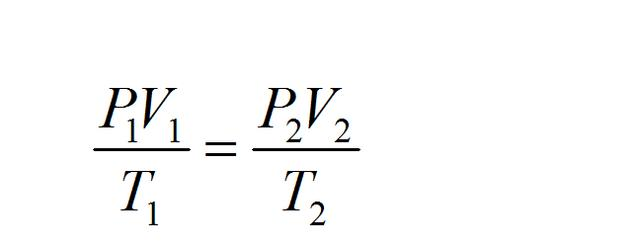
将特定气体常数 Rspecific(r) 定义为比率 R/M，

p = ρ R specific T {displaystyle p=rho R_{text{specific}}T}

这种形式的理想气体定律非常有用，因为它将压力、密度和温度联系在一个独特的公式中，与所考虑的气体的数量无关。