压缩性
编辑在热力学和流体力学中,压缩率是衡量流体或固体响应压力的瞬时相对体积变化的量度变化。 在其简单形式中,可压缩性 κ (在某些领域表示为 β)可表示为
β = − 1 V ∂ V ∂ p
其中 V 是体积,p 是压力。 选择将可压缩性定义为分数的负数使得在(通常)情况下压缩性为正,即压力增加会导致体积减小。 固定温度下压缩率的倒数称为等温体积模量。
定义
编辑上面的说明是不完整的,因为对于任何物体或系统,可压缩性的大小在很大程度上取决于过程是等熵的还是等温的。 因此,等温压缩率定义为:
β T = − 1 V ( ∂ V ∂ p ) T
其中下标 T 表示偏微分是在恒温下取的。
等熵压缩性定义为:
β S = − 1 V ( ∂ V ∂ p ) S ,
其中 S 是熵。 对于固体,两者之间的区别通常可以忽略不计。
由于材料的密度 ρ 与其体积成反比,可以证明在这两种情况下
β = 1 ρ ( ∂ ρ ∂ p ) 。
与声速的关系
编辑c 2 = ( ∂ p ∂ ρ ) S
因此,通过替换偏导数,等熵压缩率可以表示为:
β S = 1 ρ c 2
与体积模量的关系
编辑压缩率的倒数称为体积模量,通常表示为 K(有时为 B 或 β {dISPlaystyle beta } ))。压缩率方程将等温压缩率(和间接压力)与液体结构联系起来 .
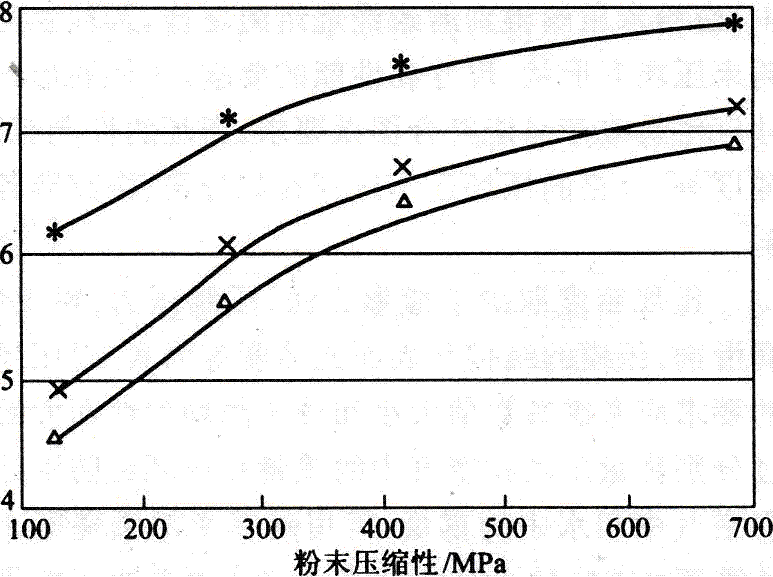
热力学
编辑等温压缩率通常通过以下几个关系与等熵(或绝热)压缩率相关:
β T β S = c p c v = γ , 其中 γ 是热容比,α 是体积热膨胀系数,ρ = N/V 是颗粒密度,Λ = ( ∂ P / ∂ T ) V为热压系数。
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/216538/
