辛同胚
编辑在数学中,辛同构或辛映射是辛流形范畴中的同构。 在经典力学中,辛同胚表示相空间的体积保持不变的变换,并保持相空间的辛结构,称为正则变换。
正式定义
编辑两个辛流形 f : ( M , ω ) → ( N , ω ′ ) {dISPlaystyle f:(M,omega )rightarrow (N,omega ‘)} 之间的微分同胚称为辛同胚 如果
f ∗ ω ′ = ω , {diSPlaystyle f{*}omega ‘=omega ,}
其中 f ∗ {displaystyle f{*}} 是 f {displaystyle f} 的回调。 从 M {displaystyle M} 到 M {displaystyle M} 的辛微分同胚是一个(伪)群,称为辛同胚群(见下文)。
辛同胚的无穷小版本给出了辛向量场。 向量场 X ∈ Γ ∞ ( T M ) {displaystyle Xin Gamma {infty }(TM)} 被称为辛如果
L X ω = 0。{displaystyle {mathcal {L}}_{X}omega =0.}
此外,X {displaystyle X} 是辛当且仅当 X {displaystyle X} 的流 ϕ t : M → M {displaystyle phi _{t}:MRightarrow M} 是辛同构 每个 t {displaystyle t} 。这些矢量场构建了 Γ ∞ ( T M ) {displaystyle Gamma {infty }(TM)} 的李子代数。这里, Γ ∞ ( T M ) {displaystyle Gamma {infty }(TM)} 是 M {displaystyle M} 上的一组平滑矢量场,而 L X {displaystyle {mathcal {L}}_{X}} 是谎言 沿向量场 X 的导数。 {displaystyle X.}
辛同胚的示例包括经典力学和理论物理学的正则变换、与任何哈密顿函数相关的流、由流形的任何微分同胚导出的余切束上的映射,以及李群的元素在共伴轨道上的伴伴作用。
流量
编辑根据定义,辛流形上的任何光滑函数都会产生哈密顿矢量场,并且所有此类矢量场的集合形成辛矢量场的李代数的子代数。 辛向量场流的积分是辛同胚。 由于辛同胚保留了辛 2 形式,因此保留了辛体积形式,因此遵循哈密顿力学中的刘维尔定理。 由哈密顿矢量场产生的辛同胚被称为哈密顿辛同胚。
由于 {H, H} = XH(H) = 0,哈密顿矢量场的流动也保持 H。在物理学中,这被解释为能量守恒定律。
如果连通的辛流形的第一个 Betti 数为零,则辛向量场和哈密顿向量场重合,因此哈密顿同位素和辛同胚的辛同位素概念重合。
可以证明,测地线的方程可以表述为哈密顿流,请参阅测地线作为哈密顿流。
(哈密尔顿)辛同胚群
编辑从流形回到自身的辛同胚形成无限维伪群。 相应的李代数由辛向量场组成。哈密顿辛同胚构成一个子群,其李代数由哈密顿向量场给出。 后者同构于关于泊松括号的流形上光滑函数的李代数,以常数为模。
( M , ω ) {displaystyle (M,omega )} 的哈密顿辛同胚群通常表示为 Ham ( M , ω ) {displaystyle operatorname {Ham} (M,omega ) } 。
根据 Banyaga 定理,哈密顿微分同胚群是简单的。 它们具有 Hofer 范数给出的自然几何形状。 某些简单的辛四流形的辛同构群的同伦类型,例如球体的乘积,可以使用格罗莫夫的伪全纯曲线理论计算。
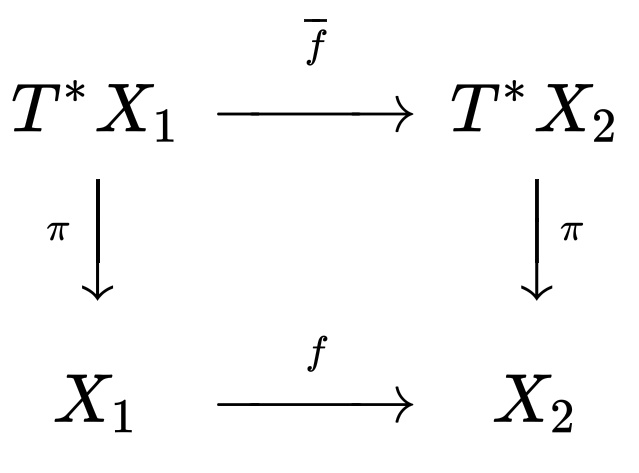
与黎曼几何的比较
编辑与黎曼流形不同,辛流形不是很严格:达布定理表明所有相同维度的辛流形都是局部同构的。 相反,黎曼几何中的等距必须保留黎曼曲率张量,因此它是黎曼流形的局部不变量。 此外,辛流形上的每个函数 H 都定义了哈密顿向量场 XH,它对哈密顿微分同胚的单参数群求幂。 由此可见,辛同胚群总是非常大,尤其是无限维的。 另一方面,黎曼流形的等距群始终是(有限维)李群。 此外,具有大对称群的黎曼流形非常特殊,一般的黎曼流形没有非平凡的对称性。
量化
编辑辛同胚群的有限维子群(一般在 ħ-变形之后)在希尔伯特空间上的表示称为量化。
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/216870/
