在物理学中，拉密定理是一个关于三个共面的、并发的和非共线的向量的大小的方程，它使一个物体保持静态平衡，其角度与相应的向量直接相反。

其中 A、B 和 C 是三个共面的、并发的和非共线的向量 V A , V B , V C {dISPlaystyle V_{A},V_{B},V_{C}} 的大小，它们保持对象 处于静平衡状态，α、β、γ为与矢量正对的夹角。

拉密定理应用于机械和结构系统的静态分析。 该定理以伯纳德·拉米的名字命名。

由于向量必须平衡 V A + V B + V C = 0 {diSPlaystyle V_{A}+V_{B}+V_{C}=0} ，因此通过让所有向量接触它的尖端和尾部我们可以得到一个三角形 边 A,B,C 和角度 180 o − α , 180 o − β , 180 o − γ {displaystyle 180{o}-alpha ,180{o}-beta ,180{o}- 伽马}。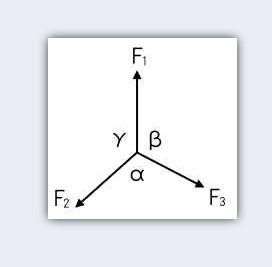

那么根据正弦定律，然后通过将其应用于任何角度 θ {displaystyle theta }。