在数学中，动力系统的本迪克森-杜拉克定理指出

在平面的单连通区域中几乎处处具有相同的符号 ( ≠ 0 {dISPlaystyle neq 0} )，则平面自治系统

没有完全位于区域内的非恒定周期解。 几乎无处不在意味着无处不在，除了可能在一组度量 0 中，例如点或线。

该定理于1901年由瑞典数学家Ivar Bendixson首先建立，1923年由法国数学家Henri Dulac利用格林定理进一步完善。

在单连通区域 R {diSPlaystyle R} 。 令 C {displaystyle C} 为平面自主系统在 R {displaystyle R} 中的闭合轨迹。 令 D {displaystyle D} 为 C {displaystyle C} 的内部。 那么根据格林定理

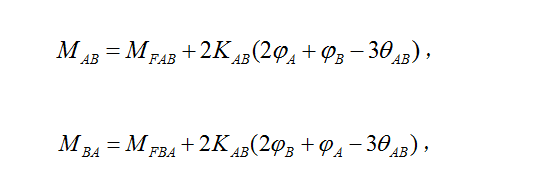
由于常量符号，上一行中的左侧积分的计算结果必须为正数。 但是在 C {displaystyle C} 上，d x = x ˙ d t {displaystyle dx={dot {x}},dt} 和 d y = y ˙ d t {displaystyle dy={dot {y}},dt} ，因此底部被积函数实际上处处为 0，因此右侧积分的计算结果为 0。这是一个矛盾，因此不可能存在这样的闭合轨迹 C {displaystyle C} 。