稳定流形定理

在数学中，特别是在动力系统和微分方程的研究中，稳定流形定理是关于逼近给定双曲不动点的轨道集结构的重要结果。 它粗略地指出，在不动点附近存在局部微分同胚意味着存在包含该不动点的局部稳定中心流形。 该流形的维数等于不动点的雅可比矩阵中小于 1 的特征值的个数。

是在 p {displaystyle p} 处具有双曲不动点的平滑映射。 我们用 W s ( p ) {displaystyle W{s}(p)} 表示稳定集，用 W u ( p ) {displaystyle W{u}(p)} 表示 p { 显示样式 p} 。

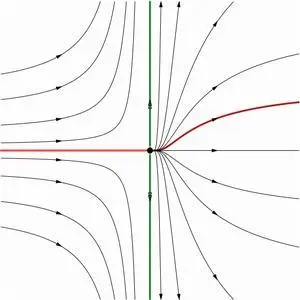
该定理指出

因此 W s ( p ) {displaystyle W{s}(p)} 是一个稳定的流形，而 W u ( p ) {displaystyle W{u}(p)} 是一个不稳定的流形。