在数学中，给定数基中的自然数是 p –卡布列克数，如果它的平方在该基数中的表示可以分成两部分，其中第二部分有 p 数字，加起来等于原始数字。

令 n 为自然数。 我们定义基数 b > 的 Kaprekar 函数 1 和幂 p >; 0

F p , b ( n ) = α + β

其中 β = n 2 mod b p 和

α = n 2 − β b p

一个自然数 n 是一个 p -卡布列克数如果它是 F p , b 的不动点，如果 F p , b ( n ) = n 。 0 和 1 是所有 b 和 p 的平凡卡布列克数，所有其他卡布列克数是 非平凡的卡布列克数。

例如，在基数 10 中，45 是一个 2-卡布列克数，因为

β = n 2 mod b p = 45 2 mod 1 0 2 = 25

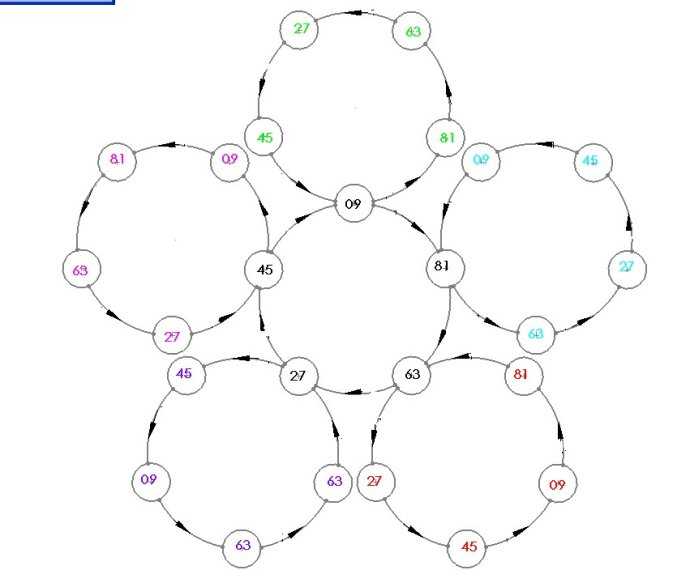
如果自然数 n 是 F p , b 的一个周期点，则它是一个社交卡布列克数，其中 F p , b k ( n ) = n 对于正整数 k是 F p 的第 k次迭代，b, 并形成周期 k 的循环。 一个卡布列克数是一个 k = 1 的社交卡布列克数，一个友好的卡布列克数是一个 k = 2 的卡布列克数 显示样式 k=2} 。

F p , b i ( n ) 到达不动点所需的迭代次数 i 是 Kaprekar 函数的持久性 n 的，如果它从未达到固定点则为未定义。

对于给定的基数 b ，只有有限数量的 p卡布列克数和循环，

我们可以将给定整数 N 的集合 K ( N ) 定义为存在自然数 A 和 B 满足丢番图方程

X 2 = A N + B ，其中 0 ≤ B <; N ，基数 b  的 n  -卡布列克数是位于集合 K ( b n ) 中的一个。