叉分岔
编辑在分岔理论(数学领域)中,干草叉分岔是一种特殊类型的局部分岔,其中系统从一个固定点过渡到三个固定点。 叉分岔,如 Hopf 分岔,有两种类型——超临界和亚临界。
在 ODE 描述的连续动力系统中——即 流——干草叉分叉通常发生在具有对称性的系统中。
超临界情况
编辑超临界干草叉分岔的正规形式是
d x d t = r x − x 3 。
亚临界情况
编辑亚临界情况的正常形式是
d x d t = r x + x 3 。
在这种情况下,对于 r <; 0 在 x = 0 处的平衡是稳定的,在 x = ± − r 平方根 {-r}}} 。 对于 r > 0 处的平衡是不稳定的。
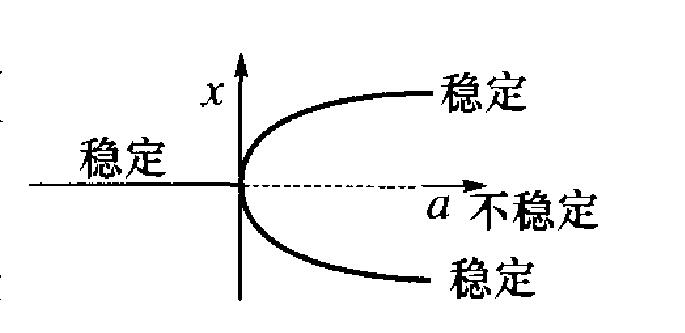
正式定义
编辑在 ( x , r ) = ( 0 , r 0 ) 处有干草叉分叉。 干草叉的形式由三阶导数的符号给出:
∂ 3 f ∂ x 3 ( 0 , r 0 ) { < 0 , 超临界 > 0 , 亚临界
请注意,亚临界和超临界描述了干草叉外线(分别为虚线或实线)的稳定性,并且不依赖于干草叉面向的方向。 例如,上面第一个 ODE 的负数 x ˙ = x 3 − r x 与第一张图片的方向相同,但相反 稳定。
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/217474/
