若斯叻吸引子

若斯吸引子 /ˈrɒslər/ 是 Rössler 系统的吸引子，Rössler 系统是一个由三个非线性常微分方程组成的系统，最初由 Otto Rössler 在 1970 年代研究。 这些微分方程定义了一个连续时间动力系统，该系统表现出与吸引子的分形特性相关的混沌动力学。

Rössler 系统的一些性质可以通过特征向量等线性方法推导出来，但系统的主要特征需要非线性方法，如 Poincaré 映射和分岔图。 Rössler 的原始论文指出若斯吸引子的行为类似于洛伦兹吸引子，但也更易于定性分析。 吸引子内的轨道沿着靠近不稳定固定点的 x , y {displaystyle x,y} 平面的向外螺旋运动。 一旦图形螺旋足够大，第二个固定点就会影响图形，导致 z {displaystyle z} 维度上升和扭曲。 在时域中，很明显，尽管每个变量都在固定值范围内振荡，但振荡是混乱的。 该吸引子与洛伦兹吸引子有一些相似之处，但更简单并且只有一个流形。 奥托·罗斯勒 (Otto Rössler) 于 1976 年设计了若斯吸引子，但后来发现最初的理论方程可用于模拟化学反应的平衡。

使用拓扑分析研究了参数空间的另一条线。 它对应于 b = 2 {displaystyle b=2} , c = 4 {displaystyle c=4} ，并且选择 {displaystyle a} 作为分叉参数。 Lössler 是如何发现这组方程的，Letellier 和 Messager 对此进行了研究。

若斯吸引子的一些优雅是由于它的两个方程是线性的； 设置 z = 0 {displaystyle z=0} ，允许检查 x , y {displaystyle x,y} 平面上的行为

特征值是复数并且都具有正实数分量，使得原点在 x , y {displaystyle x,y} 平面上向外螺旋不稳定。 现在考虑 z {displaystyle z} 平面行为在此范围内的 a {displaystyle a} 。

为了找到固定点，将三个 Rössler 方程设置为零，并确定每个固定点的

通过求解得到的方程。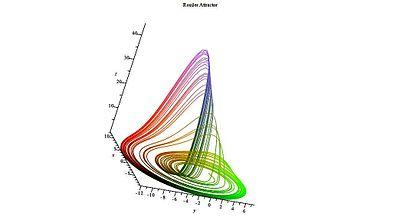

这反过来又可以用来显示一组给定参数值的实际固定点

如上面 Rössler Attractor 的一般图所示，这些固定点之一位于吸引子环的中心。