联合熵
编辑在信息论中,联合熵是与一组变量相关的不确定性的度量。
定义
编辑两个离散随机变量 X和 Y 与图像 X和 Y 定义为
(等式 1)
其中 x和 y 分别是 X 和 Y 的特定值,P ( x , y )是这些值一起出现的联合概率,P ( x , y ) log 2 [ P ( x , y ) ] 如果 P ( x , y ) = 0 ,[P(x,y)]} 被定义为 0。
对于两个以上的随机变量 X 1 , . . . , X n 这扩展为
(等式 2)
其中 x 1 , . . . , x n是 X 1 , 的特定值。 . . , X n ,分别为 P ( x 1 , . . . , x n ) 是这些值一起出现的概率,P
属性
编辑非负性
编辑一组随机变量的联合熵是一个非负数。
大于个体熵
编辑一组变量的联合熵大于或等于该集合中变量的所有单个熵的最大值。
小于等于个体熵之和
编辑一组变量的联合熵小于或等于该集合中变量的个体熵之和。 这是次可加性的一个例子。 当且仅当 X {dISPlaystyle X} 和 Y {diSPlaystyle Y} 在统计上独立时,这个不等式才是等式。
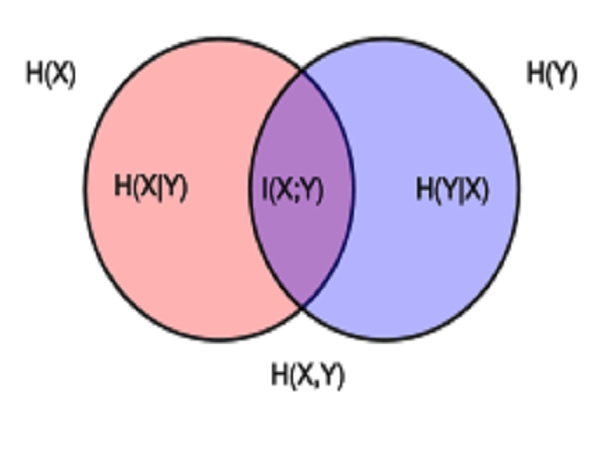
与其他熵测量的关系
编辑条件熵的定义中使用了联合熵
H ( X | Y ) = H ( X , Y ) − H ( Y )
在量子信息论中,联合熵被推广为联合量子熵。
联合微分熵
编辑定义
编辑上述定义适用于离散随机变量,在连续随机变量的情况下同样有效。 离散联合熵的连续版本称为联合微分(或连续)熵。 设 X 和 Y 是具有联合概率密度函数 f ( x , y ) 的连续随机变量。 微分联合熵 h ( X , Y ) 定义为
(等式 3)
对于两个以上的连续随机变量 X 1 , . . . , X n 的定义概括为:
(等式4)
积分接管 f的支持。 有可能积分不存在,在这种情况下我们说微分熵没有定义。
属性
编辑在离散情况下,一组随机变量的联合微分熵小于或等于各个随机变量的熵之和:
h ( X 1 , X 2 , … , X n ) ≤ ∑ i = 1 n h ( X i )
以下链式规则适用于两个随机变量:
h ( X , Y ) = h ( X | Y ) + h ( Y )
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/217560/
