波塞利耶-利普金机械

波塞利耶-利普金机械是xxx个真正的平面直线机构——xxx个能够将旋转运动转化为完美直线运动的平面连杆机构，反之 反之亦然。

在本发明之前，没有参考导轨，不存在将精确的直线运动转换为圆周运动的平面方法。 1864 年，所有动力都来自蒸汽机，蒸汽机有一个活塞在汽缸中上下直线运动。 该活塞需要与气缸保持良好的密封以保留驱动介质，并且不会因泄漏而损失能量效率。 活塞通过保持垂直于气缸的轴线并保持其直线运动来做到这一点。 将活塞的直线运动转换为圆周运动至关重要。 大多数这些蒸汽机的应用都是旋转的。

有一种更早的直线机制，其历史并不为人所知，称为 Sarrus linkage。 这种连杆比 Peaucellier-Lipkin 连杆早了 11 年，由一系列铰接的矩形板组成，其中两个保持平行，但可以正常地相互移动。 Sarrus 的连杆机构属于三维类，有时称为空间曲柄，这与平面机构的 Peaucellier-Lipkin 连杆机构不同。

在仪器的几何图中，可以看到六个固定长度的杆：OA、OC、AB、BC、CD、DA。 OA的长度等于OC的长度，AB、BC、CD、DA的长度都相等，构成一个菱形。 另外，O点是固定的。 然后，如果 B 点被约束沿着穿过 O 的圆移动，则点 D 将必然必须移动 沿着一条直线。 另一方面，如果 B 点被迫沿直线移动，则 D 点必然必须沿圆移动。

首先，必须证明点O、B、D共线。 通过观察连杆机构关于线 OD 镜像对称，可以很容易地看出这一点，因此点 B 必须落在该线上。

更正式地说，三角形 △BAD 和 △BCD 是全等的，因为边 BD 与自身全等，边 BA 与边 BC 全等，边 AD 与边 CD 全等。 因此，角∠ABD 和∠CBD 相等。

其次，三角形△OBA和△OBC全等，因为边OA和OC全等，边OB全等，边BA和BC全等。 因此，角∠OBA 和∠OBC 相等。

最后，因为它们形成一个完整的圆，我们有

∠ O B A + ∠ A B D + ∠ D B C + ∠ C B O = 360 ∘

令点 P 为直线 AC 和 BD 的交点。 那么，由于 ABCD 是菱形，P 是线段 BD 和 AC 的中点。 因此，长度BP = 长度PD。

三角形△BPA全等三角形△DPA，因为边BP全等边DP，边AP全等于自身，边AB全等边AD。 因此，角∠BPA = 角∠DPA。 但由于∠BPA + ∠DPA = 180°，则2 × ∠BPA = 180°，∠BPA = 90°，∠DPA = 90°。

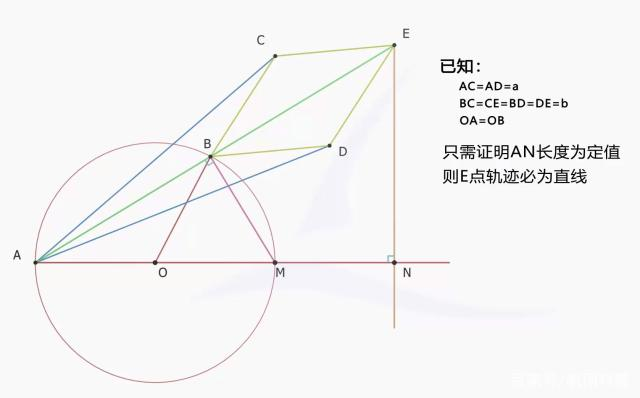
由于OA和AD都是固定长度，那么OB和OD的乘积是一个常数：

ℓ O B ⋅ ℓ O D = k 2

并且由于点 O、B、D 共线，则 D 是 B 的倒数。