半峰全宽

在分布中，半峰全宽 是因变量等于其xxx值的一半时自变量的两个值之间的差值。 换句话说，它是在 y 轴上的那些点之间测量的频谱曲线的宽度，这些点是xxx幅度的一半。如果函数是对称的，则半峰半宽 是 FWHM 的一半。术语全 当自变量是时间时，半xxx值持续时间 是首选。

FWHM 适用于脉冲波形的持续时间和用于光通信的光源的光谱宽度以及光谱仪的分辨率等现象。宽度表示半xxx值的约定也广泛用于信号处理中，将带宽定义为频率范围的宽度 其中不到一半的信号功率被衰减，即功率至少是xxx值的一半。 在信号处理方面，这最多是 −3 dB 的衰减，称为半功率点，或者更具体地说，半功率带宽。当半功率点应用于天线波束宽度时，称为半功率波束宽度 .

如果考虑的函数是正态分布的密度，形式为 f ( x ) = 1 σ 2 π exp ⁡ [ − ( x − x 0 ) 2 2 σ 2 ] 其中σ为标准差，x0为期望值，则FWHM与标准差的关系为F W H M = 2 2 ln ⁡ 2 σ ≈ 2.355 σ 。 此 FWHM 内的相应区域占 大约76%。宽度不依赖于期望值x0； 它在平移下是不变的。如果高斯函数的 FWHM 已知，则可以通过简单的乘法对其进行积分。

在光谱学中，通常使用半峰宽的一半（此处为 γ）HWHM。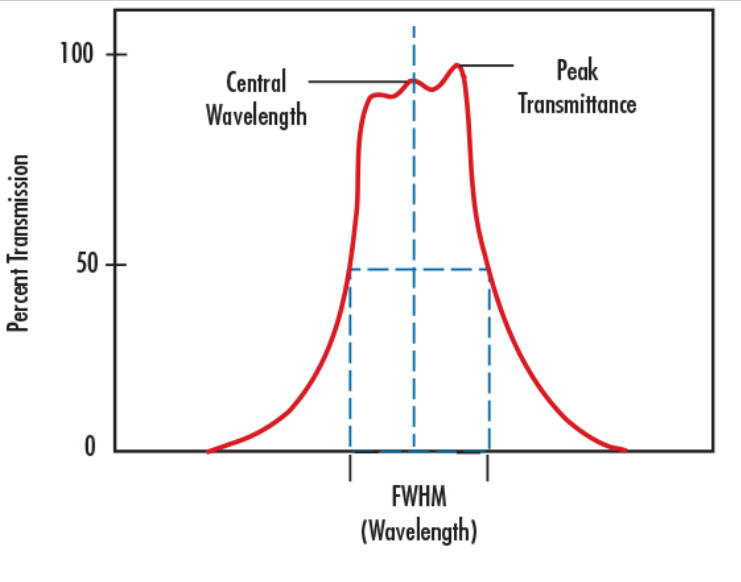

与光学中的孤子相关的另一个重要分布函数是双曲正割：f ( x ) = sech ⁡ ( x X ) 。 任何翻译元素都被省略了，因为它不影响 FWHM。 对于这个冲量，我们有： F W H M = 2 arsech ⁡ ( 1 2 ) X = 2 ln ⁡ ( 2 + 3 ) X ≈ 2.634 X 其中 arsech 是 反双曲正割。