在凝聚态物理学中，阿罗特图是物质的磁化强度 M 2 {dISPlaystyle M{2}} 的平方与外加磁场与磁化强度 H / M { diSPlaystyle H/M} 在一个（或多个）固定温度下。 阿罗特图是一种确定材料中是否存在铁磁有序的简单方法。 它们以美国物理学家 Anthony Arrott 的名字命名，他于 1957 年将它们作为一种研究磁学的技术引入。

根据应用于磁性平均场图的 LANDau 理论，接近相变的铁磁材料的自由能可写为：

F ( M ) = − H M + a T − T c T c M 2 + b M 4 + … {displaystyle F(M)=-HM+a{frac {T-T_{c}}{T_ {c}}}M{2}+bM{4}+ldots }

其中 M {displaystyle M} ，磁化强度，是有序参数， H {displaystyle H} 是施加的磁场， T c {displaystyle T_{c}} 是临界温度，而 a , b {displaystyle a,b} 是材料常数。

接近相变，这给出了磁化顺序参数的关系：

M 2 = 1 4 b H M − a 2 b ϵ {displaystyle M{2}={frac {1}{4b}}{frac {H}{M}}-{frac {a }{2b}}epsilon }

其中 ε = T − T c T c {displaystyle epsilon ={frac {T-T_{c}}{T_{c}}}} 是温度的无量纲量度。

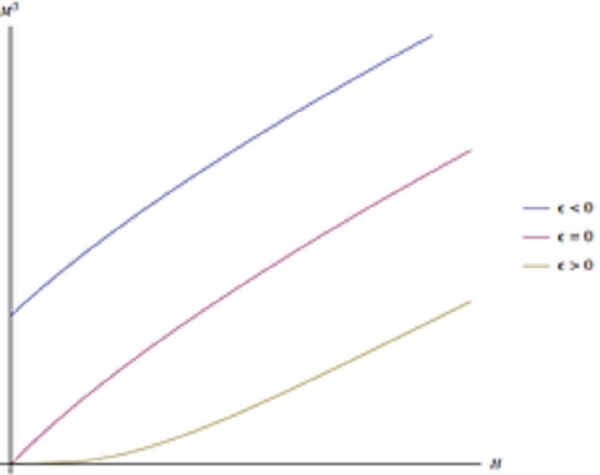
因此，在针对不同温度绘制 M 2 {displaystyle M{2}} 与 H / M {displaystyle H/M} 的图表中，没有截距的线对应于临界温度下的相关性。 因此，除了为铁磁相的存在提供证据外，阿罗特图还可以用来确定相变的临界温度。

在状态方程中明确给出临界指数

其中 T 1 , M 1 , γ , β {displaystyle T_{1},M_{1},gamma ,beta } 是自由参数。 在这些修改过的阿罗特图中，数据绘制为 M 1 / β {displaystyle M{1/beta }} 与 ( H / M ) 1 / γ {displaystyle (H/M){1 /伽马}}。 在经典朗道理论的情况下，β = 1 / 2 {displaystyle beta =1/2} 和 γ = 1 {displaystyle gamma =1} 并且这个等式简化为线性 M 2 { displaystyle M{2}} 与 H / M {displaystyle H/M} 图。 然而，该方程还允许 γ {displaystyle gamma } 和 β {displaystyle beta } 的其他值，因为真实的铁磁体通常没有与简单的平均场理论铁磁性完全一致的临界指数。

对给定系统使用正确的临界指数有助于在 Arott 图上给出直线，但在低磁场和非晶材料等情况下则不然。 虽然平均场理论对于较高磁场下的铁磁体是一种更合理的模型，但实际磁体中存在多个磁畴意味着特别是在低磁场下，实验测量的宏观磁场（这是整个样品的平均值 ) 将不是确定局部磁场（由单个原子感受到）的合理方法。 因此，为了阿罗特图的目的，应忽略在低磁场下获取的磁化数据。

磁相变可以是一阶或二阶。 过渡的性质可以根据磁等温线的斜率从阿罗特图中推断出来。 如果线都是正斜率，则相变为二阶，而如果有负斜率线，则相变为一阶。 这种情况称为 Banerjee 标准。

Banerjee 准则对于评估非均匀铁磁体并不总是准确的，因为即使跃迁是一阶的，斜率也可能都是正的。