范德华方程

在化学和热力学中，范德华方程（或范德华方程）是一个状态方程，它扩展了理想气体定律以包括气体分子之间相互作用的影响，并考虑了分子的有限尺寸。

理想气体定律将气体分子视为与其容器相互作用但彼此不相互作用的点粒子，这意味着它们在碰撞期间既不占用空间也不改变动能（即所有碰撞都是完全弹性的）。 理想气体定律指出，由 n 摩尔任何气体占据的体积 V 在温度 T 下的压力 P 由以下关系给出，其中 R 是气体常数：

P V = n R T {\displaystyle PV=nRT}

为了计算真实气体分子所占据的体积，范德华方程将理想气体定律中的 V / n {\displaystyle V/n} 替换为 ( V m − b ) {\displaystyle (V_{m}-b) } ，其中 Vm 是气体的摩尔体积

对理想气体定律的第二个修改说明了气体分子之间的相互作用。 范德华方法通过在状态方程中观察到的压力 P 添加一个形式为 a / V m 2 {\displaystyle a/V_{m}{2}} 的项来包括分子间相互作用，其中 a 是一个常数，其值 取决于气体。

当摩尔体积Vm很大时，b相对于Vm可以忽略不计，a/Vm2相对于P可以忽略不计，范德华方程简化为理想气体定律，PVm=RT。

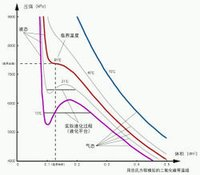
该方程近似于实际流体在其临界温度以上的行为，并且对于它们在低温下的液态和低压气态在定性上是合理的。 然而，在气液之间的相变附近，在 p、V 和 T 范围内，液相和气相处于平衡状态，范德华方法无法准确模拟观察到的实验行为。 特别是，p 是这些区域中给定温度下 V 的常数函数。 因此，范德瓦尔斯模型对于旨在预测临界点附近区域的真实行为的计算没有用处。 解决这些预测缺陷的修正包括等面积规则和相应状态的原则。

该方程式以其开发者荷兰物理学家约翰内斯·迪德里克·范德瓦尔斯的名字命名。

范德华方程是一种热力学状态方程，基于以下理论：流体由具有非零体积的粒子组成，并受到（不一定成对的）粒子间吸引力。