共变导数
编辑在数学中,协变导数是一种指定沿流形的切向量的导数的方法。 或者,协变导数是一种通过微分算子在流形上引入和处理连接的方法,与框架丛上的主连接给出的方法形成对比——参见仿射连接。 在流形等距嵌入高维欧氏空间的特殊情况下,协变导数可以看作是欧氏方向导数在流形切线空间上的正交投影。 在这种情况下,欧几里德导数被分成两部分,外在正常分量(取决于嵌入)和内在协变导数分量。
这个名字的动机是坐标变化在物理学中的重要性:协变导数在一般坐标变换下进行协变变换,即通过变换的雅可比矩阵线性变换。
本文介绍了矢量场相对于矢量场的协变导数,既使用坐标自由语言,也使用局部坐标系和传统索引符号。 张量场的协变导数作为同一概念的扩展呈现。 协变导数直接概括为与向量丛上的连接相关联的微分概念,也称为 Koszul 连接。
历史
编辑关键特征不是对度量的特别依赖,而是 Christoffel 符号满足某种精确的二阶变换法则。 这种变换法则可以作为以协变方式定义导数的起点。 因此,协变微分理论从严格的黎曼语境中分离出来,包括更广泛的可能几何。
Koszul 连接消除了在微分几何中对 Christoffel 符号(和其他类似的非张量对象)进行笨拙操作的需要。
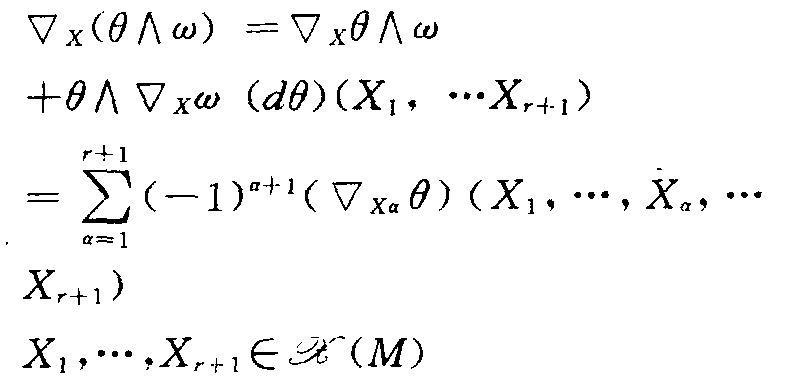
动机
编辑协变导数是向量微积分的方向导数的推广。与通常的方向导数的主要区别是 ∇ u v {dISPlaystyle nabla _{mathbf {u} }{ mathbf {v} }} 必须在某种精确意义上独立于它在坐标系中的表达方式。
一个向量可以被描述为一个基于基的数字列表,但作为一个几何对象,无论它如何被描述,向量都保持其身份。 对于一个基写成分量的几何向量,当基改变时,分量根据基公式的变化进行变换,坐标进行协变变换。
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/221289/
