移动平均

移动平均线（也称移动平均线）是一种平滑时间或数据序列的方法。 平滑是通过去除较高频率的分量来完成的。 结果，创建了一组新的数据点，它由原始数据点集的大小相等的子集的平均值组成。 在信号理论中，移动平均值被描述为有限脉冲响应 (FIR) 低通滤波器。 在等权形式中，移动平均值代表最简单的 FIR 低通滤波器。

例如，在时间序列分析中使用移动平均线。 等权重变体对应于具有矩形函数的卷积，并导致许多问题，例如可以用特殊权重来抵消。

一组移动平均线是在给定信号的一个部分（“窗口”）上迭代（“移动”）计算的。 使用的窗口以重叠方式移动，即。 换句话说，重复删除所考虑部分的最后一个值，添加该部分之后的xxx个值并计算新的平均值。 为了计算平均值，可以根据需要对窗口中的值进行加权。

均值的结果集是独立的。 但是，它通常与输入集中称为“热点”的位置相关联。 热点可以在窗口区域，但不一定是。 在时间序列的情况下，最后一个时间点通常被用作热点； 在其他应用程序中，居中映射很常见。

离散时间序列 x ( t )的第 n 阶的简单移动平均线（SMA）是 n {displaystyle n 的算术平均值序列} 连续的数据点。 既然是时间序列，那么热点就是最后一个时间点。 以下解释均针对此特殊情况。

类似于具有有限脉冲响应的滤波器， n + 1 也称为阶数。

这样的移动平均线有延迟（群延迟）为 τ = n − 1 2 ，平均值滞后 τ 时间单位。

这种滞后可以通过将移动平均线移动 τ 来纠正。 这就是所谓的中心平均。 但是随后就没有更多的xxx个和最后一个 τ 时间单位的值了。 在不使用动态窗口的情况下，只能通过使用低阶、不同的权重或估计器来缩小或至少减少这种差距。

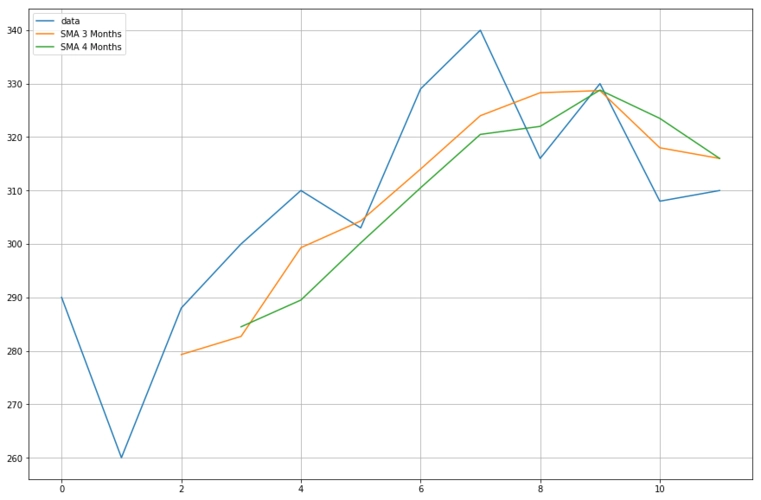
移动平均滤波器是低通滤波器，但个别频率范围或多或少被过滤，并且会发生信号偏移（滞后）。

离散集合 x ( t ) 阶移动平均线 | x ( t ) | {displaystyle |x(t)|} 元素有 n − 1 {displaystyle n-1} 对值小于总集合。 由于非常强烈的振荡图需要相应的高阶来充分平滑结果集，因此这种效果会对显示产生显着影响。 由此产生的趋势线越来越多地与未居中的简单移动平均线相抵消，因此反映了原始数据越来越差的抽象。

平滑曲线是一条有意义但明显偏移的趋势线。 此外，丢失了 20% 的值对。 在动态窗口的帮助下，可以在 x ( t ) {displaystyle x(t)} 的整个宽度上计算值。