戴克斯特拉算法

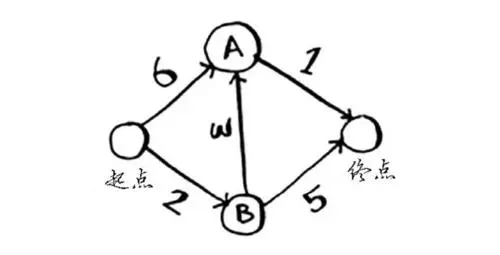
戴克斯特拉算法，是贪婪算法类中的一种算法，用于解决给定起始节点的最短路径问题。 因此，它计算给定起始节点与边加权图中剩余节点之一（或所有）之间的最短路径（前提是它不包含负边）。

对于断开连接的无向图，从起始节点到没有路径的那些节点的距离是无限的。 对于非强连通的有向图也是如此。 该距离也同义地称为距离、成本或重量。

该算法的基本思想是始终遵循从起始节点到承诺最短路径的边。 只有在考虑了所有较短的路线段（也超出其他节点）后，才会遵循其他边。 此过程确保当到达一个节点时，没有更短的路径可以到达它。 一旦计算出起始节点和访问节点之间的距离，就将其存储起来。 另一方面，到尚未处理的节点的总距离在算法过程中肯定会发生变化，即减少。 继续此过程，直到计算出到目标节点的距离（单对最短路径）或已知所有节点到起始节点的距离（单源最短路径）。

该算法可以通过以下步骤来描述。 计算最短（加起来）距离及其节点序列。

• 将“距离”和“前任”这两个属性（属性）分配给所有节点。 用 0 初始化起始节点中的距离，用 ∞ 初始化所有其他节点中的距离。
• 只要还有未访问的节点，选择距离最小（累积）的节点
• 保存该节点已经被访问过。
• 使用相应的边权重和已计算的从起始节点到当前节点的距离之和，计算所有尚未访问的相邻节点的总距离。
• 如果节点的此值小于存储在那里的距离，则更新它并将当前节点设置为前任节点。此步骤也称为更新或松弛。

在这种形式中，算法计算从起始节点开始到所有其他节点的最短路径。 另一方面，如果您只对到一个非常具体的节点的路径感兴趣，那么如果您正在寻找的节点是活动节点，您就可以在步骤 (2) 中中止。

由于一旦设置到起始节点的距离就不会改变，戴克斯特拉算法属于贪心算法，在每一步中优先选择当前最有希望的部分解决方案。 然而，与其他一些贪心算法不同，戴克斯特拉算法总是计算出一个最优解。 此属性基于路径中节点之间的最短跳数组合形成该路径上的最短路径的假设。 如果边权重为正，则该假设是有效的，因为如果稍后发现从起始节点到目标节点的较短路径，则也必须更早地检查较短的路段才能正确执行算法。 但是你会在较短的路线上比在较长的路线上更早地找到目的地节点。

但是，如果图形包含负边权重，则该假设不再成立。 然后每个部分可以是端点之间的最短部分，但如果负边缘再次减少路径长度，则可以改善较长部分的总距离。

以下几行伪代码描述了一个名为 Dijkstra 的函数，该函数将图形和图形中的起始节点作为输入。 起始节点指定从中寻找到所有节点的最短路径的节点。 结果是一个列表，为每个节点 v 提供从起始节点到 v 的前任节点。

如果两个节点之间存在边，则这些节点是邻居。 当前在子步骤中考虑的节点用 u 表示，称为“观察节点”。 可能即将到来的相邻节点是en 在各自即将进行的中期调查中，每个 v 作为“测试节点”。

distance 的数值包含了检查分支中各自的总距离，它是将起点经过可能的中间节点和当前节点 u 到下一个待检查节点 v 的部分距离相加。

首先，根据图和起始节点初始化距离和前驱。 这是在初始化方法中完成的。

初始化将距离设置为无穷大，将前身设置为未知。 只有起始节点的距离为 0。集合 Q 包含尚未找到最短路径的节点。

1 方法初始化（图形，开始节点，距离，前身，Q）：对于图形中的每个节点 v 2：3 距离：= 无穷大 4 祖先：= 零 5 距离：= 0 6 Q：= 图形中的所有节点

如果通过 u 到 v 的路径比先前已知的路径短，则从起始节点到节点 v 的距离会缩短。 相应地，u 在最短路径上成为 v 的前导。

如果您只对两个节点之间的最短路径感兴趣，则可以在 Dijkstra 函数的第 5 行 if u = destination node 之后停止算法。

节点和节点之间的边通常可以用矩阵或指针结构来表示。 指针也可以引用节点的前驱。 节点的距离可以存储在字段中。

为了有效实现，尚未找到最短路径的节点集合 Q 由优先级队列实现。 耗时的初始化只发生一次，但对 Q 的重复访问效率更高。 它各自的距离，在带有距离的伪代码中指定，用作节点的键值。 如果距离减小，则需要对队列进行部分重新安排。

距离表或邻接矩阵是适用于此的数据结构。

下面的 C++ 编程语言示例显示了戴克斯特拉算法对于存储为邻接表的无向图的实现。 执行程序时，会用到main函数，在控制台输出一条最短路径。

另一种依赖贝尔曼最优性原则的最短路径搜索算法是 Floyd-Warshall 算法。 最优性原则指出，如果从 A 到 C 的最短路径是经过 B，则部分路径 AB 也必须是从 A 到 B 的最短路径。