累积和

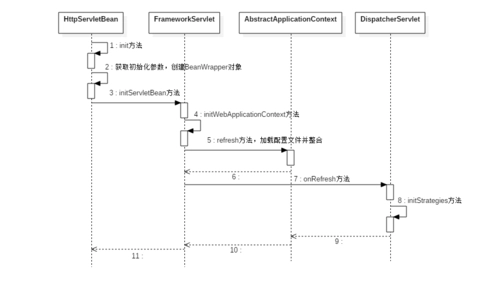
在统计过程和质量控制中，累积和或累积和，是一种顺序分析方法，用于检测顺序数据序列或时间序列中的变化（例如过程变化或转折点）。

累积和考虑数据值 x n和给定值 ω n 的累积和：

S 0 = 0 {\displaystyle S_{0}=0}S n = max ( 0 , S n − 1 + x n − ω n ) {\displaystyle S_{n}=\max(0,S_{n-1} +x_{n}-\omega _{n})}

需要注意的是，累积和不仅仅是数据值的累加和，而是数据值 x n  和 ω n  。 如果 S n + 1 的值超过给定的极限值，那么就发现了变化。 累积和不仅识别急剧的数据值变化，而且在观察期间逐步连续。 大多数情况下， ω 是一个似然函数，尽管 Page 的文章没有这样指定。

在示例中，指定了 ω n = 5 {\displaystyle \omega _{n}=5} 并且考虑了正负累积偏差：

S 0 = S 0 + = S 0 − = 0

S n  也可以解释为：

• 所有数据点都经过均值调整 ( x n − ω n {\displaystyle x_{n}-\omega _{n}} ) 和
• 所有先前的均值调整差异都添加到每个新创建的值中。

均值是对正态分布数据值的期望值的似然估计。

下图显示了 S n {\displaystyle S_{n}\,} , S n + {\displaystyle S_{n}^{+}} 和 S n − {\displaystyle S_{n}^{-} } 在不同的情况下：

• 左：过程的均值不变
• 中间：过程的均值缓慢增加（相对于分布）
• 右：均值在 60​​ 个时间单位后突然上升

这些变化在数据中几乎看不到，但在 S n {\displaystyle S_{n}\,} , S n + {\displaystyle S_{n}^{+}} 和 S n − {\displaystyle S_{n}^{-}} 曲线。