残差平方和
编辑残差平方和,是指所有观测值的平方(最小二乘)残差(观测值与预测值之间的偏差)之和。 由于首先形成偏差平方(此处为残差平方),然后对所有观测值求和,因此表示偏差平方和。残差平均值是线性模型的质量标准,描述了模型的不准确性。 它捕获了观察值围绕目标变量的预测值的散布,即样本回归线无法解释的散布。 因此也称为不明偏差平方和(或简称不明偏差平方和)。 除了残差平方和,总平方和和解释平方和在统计中也起着重要作用。
要执行全局 F 检验,通常需要均方。 如果将残差水平和除以残差自由度,则得到平均残差平方。 然后,全局 F 检验的检验统计量由“解释偏差的均方”与“残差的均方”的商给出。
计算示例
编辑下面的例子应该显示残差水平和的计算。 随机抽取10艘战舰(见战舰数据),按长宽(米)进行分析。 考察一艘军舰的宽度是否可能与长度有固定关系。
散点图表明船的长度和宽度之间存在线性关系。 使用最小二乘估计执行的简单线性回归给出绝 对项 β ^ 0 = − 8.645 0715。
该等式表示估计宽度 y ^ = b r e i t e ^ {dISPlaystyle, 作为长度的函数 x = l a ¨ n g e. 该函数显示所选战舰的宽度大约是其长度的六分之一。
除了测量值的总平方和574.849 m 2外,表格还显示残差平方和(最后列)44.740 5 m 2 阅读。 基于这两个变量,还可以计算决定系数。
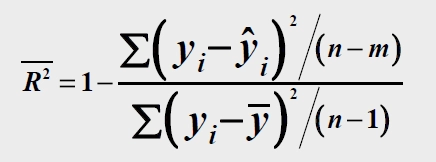
残差平方和的属性
编辑残差平方和分布
如果观测值呈多维正态分布,则残差平均值和 S Q R 与误差方差 σ 2 的商服从卡方分布,其中 n − p,自由度如下:
S Q R σ 2 = ε ^ ⊤ ε ^ σ 2 = ( n − p ) σ ^ 2 σ 2 ∼ χ 2 ( n − p )
其中 σ ^ 2 表示干扰变量方差的无偏估计。
残差水平和的期望值
可以证明残差平面和 σ 2 ( n − k − 1 ) {diSPlaystyle sigma ^{2}(n-k-1)} 结果的期望值
E ( ε ^ ⊤ ε ^ ) = E ( ε ⊤ ( I − X ( X ⊤ X ) − 1 X ⊤ ) ε ) = σ 2 ( n − k − 1 )
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/363591/
