目录
活塞运动方程
编辑通过连杆连接到旋转曲柄的非偏置活塞的往复运动(如在内燃机中发现的那样)可以用运动方程表示。本文展示了如何使用微积分作为角度(角度域)和时间(时域)的函数来导出这些运动方程。
关于角位置的方程(角域)
编辑角度域方程表示为角度的函数。
导出角域方程
编辑活塞往复运动的角域方程由系统的几何方程推导出如下。
非简谐运动
编辑上面的角域方程表明活塞(连接到连杆和曲柄)的运动不是简单的谐波运动,而是随着曲柄的旋转而受到连杆运动的修正。这与直接产生简谐运动的苏格兰轭形成对比。
关于时间的方程(时域)
编辑时域方程表示为时间的函数。
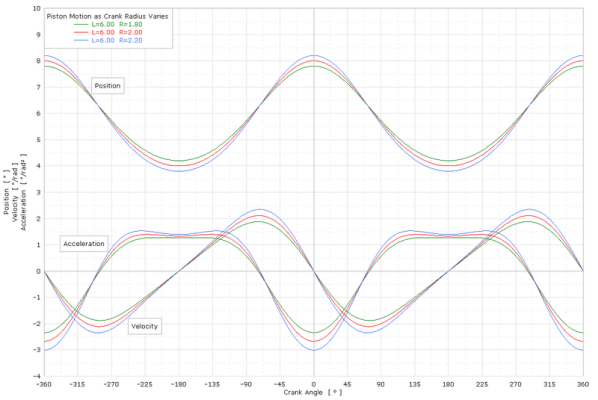
曲柄杆角度不是直角
编辑当曲柄与杆成直角时,不一定会出现速度最大值和最小值。存在反例来反驳陈述速度最大值和最小值仅在曲柄杆角度为直角时出现。
方便单位
请注意,对于汽车/热车用例,活塞杆曲柄几何形状最方便(爱好者使用)的长度单位是英寸,典型尺寸是6(英寸)杆长度和2(英寸)曲柄半径.本文使用英寸()为单位来表示位置、速度和加速度。
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/147701/
