递归定义

在数学和计算机科学中，递归定义，或归纳定义，是用来用一个集合中的其他元素来定义该集合中的元素（Aczel1977:740ff）。一些可递归定义对象的例子包括阶乘、自然数、斐波那契数和康托尔三元集。一个函数的递归定义是根据其他（通常是较小的）输入的同一函数的值来定义该函数对某些输入的值。例如，阶乘函数n！是由以下规则定义的0!=1.(n+1)!=(n+1)-n！。这个定义对每个自然数n都有效，因为递归最终会达到0这个基数。这个定义也可以被认为是给出了一个计算函数n！值的程序，从n=0开始，一直到n=1、n=2、n=3等。递归定理指出，这样的定义确实定义了一个xxx的函数。该证明使用了数学归纳法。一个集合的归纳定义用集合中的其他元素来描述集合中的元素。例如，自然数集合N的一个定义是：1在N中。如果一个元素n在N中，那么n+1就在N中。N是满足(1)和(2)的所有集合的交集。有许多集合满足(1)和(2)--例如，集合{1,1.649,2,2.649,3,3.649,...}就满足这个定义。然而，条件(3)通过去除不相干成员的集合来指定自然数的集合。请注意，这个定义假定N包含在一个更大的集合（如实数集合）中--在这个集合中定义了操作+。递归定义的函数和集合的属性通常可以通过遵循递归定义的归纳原则来证明。例如，这里介绍的自然数的定义直接意味着自然数的数学归纳原则：如果一个属性对自然数0（或1）成立，并且只要对n成立，该属性就对n+1成立，那么该属性就对所有自然数成立（Aczel1977:742）。

大多数递归定义有两个基础：一个基例（basis）和一个归纳句。循环定义和递归定义的区别在于，递归定义必须总是有基例，即满足定义的情况，而不需要用定义本身来定义，而且归纳子句中的所有其他实例必须在某种意义上更小（即更接近那些终止递归的基例）--这一规则也被称为只用更简单的案例来递归。相反，一个循环定义可能没有基例，甚至可能以一个函数的值本身来定义该值--而不是以该函数的其他值来定义。这样的情况会导致无限倒退。递归定义是有效的，也就是说，一个递归定义可以确定一个xxx的函数，这是集合论的一个定理，被称为递归定理，其证明是不简单的。当函数的域是自然数时，定义有效的充分条件是给出了f(0)的值（即基数），并且对于n>0，给出了用n、f(0)、f(1)、...、f(n-1)确定f(n)的算法（即归纳条款）。

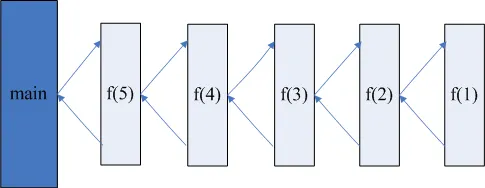
更一般地说，只要域是一个有秩序的集合，就可以利用转折递归的原则对函数进行递归定义。对于一般情况来说，构成有效递归定义的形式标准更为复杂。一般证明和标准的概要可以在JamesMunkres的《拓扑学》中找到。然而，下面将给出一般递归定义的一个特殊情况（域被限制为正整数，而不是任何有秩序的集合）。

设A是一个集合，设a0是A的一个元素。如果ρ是一个函数，它为映射正整数的非空部分到A的每个函数f分配A的一个元素，那么存在一个xxx的函数{displaystyleh(i)=rho(h|_{{1,2,ldots,i-1}){text{for}}i>1.}。递归定义的例子初级函数加法是基于计数的递归定义.