枚举算法

在计算机科学中，枚举算法是一种对计算问题的答案进行枚举的算法。从形式上看，这种算法适用于接受一个输入并产生一个解决方案列表的问题，类似于函数问题。对于每个输入，枚举算法必须产生所有解决方案的列表，没有重复的，然后停止。枚举算法的性能是以产生解决方案所需的时间来衡量的，可以是产生所有解决方案所需的总时间，也可以是两个连续解决方案之间的xxx延迟，还可以是预处理时间，算作输出xxx个解决方案前的时间。这种复杂性可以用输入的大小、每个单独输出的大小或所有输出集合的总大小来表示，与输出敏感算法的做法类似。

在计算复杂性理论的背景下，枚举问题已经被研究过了，并且已经为这类问题引入了几个复杂性类。一个非常普遍的类是EnumP，这类问题的可能输出的正确性可以在输入和输出的多项式时间内被检查出来。形式上，对于这样的问题，必须存在一个算法A，它将问题输入x，候选输出y作为输入，并以x和y的多项式时间解决y是否为输入x的正确输出的决策问题。其他被定义的类包括如下。在同样属于EnumP的问题的情况下，这些问题从最小到xxx体排序输出多项式，这类问题的完整输出可以在多项式时间内计算出来。增量多项式时间，这类问题，对于所有的i，第i个输出可以在输入大小和数字i的多项式时间内产生。多项式延迟，这类问题中两个连续输出之间的延迟是输入的多项式（与输出无关）。强多项式延迟，这类问题中每个输出前的延迟是这个特定输出大小的多项式（与输入或其他输出无关）。通常假设预处理是多项式的。恒定延迟，这类问题中每个输出前的延迟是恒定的，即与输入和输出无关。预处理阶段一般假设为输入的多项式。常用技术回溯。列举所有解决方案的最简单方法是系统地探索可能的结果空间（在每个连续的步骤中对其进行分割）。然而，这样做可能不能很好地保证延迟，也就是说，回溯算法可能会花很长的时间去探索部分可能的结果空间，而这些结果并不能产生一个完整的解决方案。闪光搜索。这种技术通过探索所有可能的解决方案的空间来改进反向追踪，但在每一步都要解决当前的部分解决方案是否可以扩展为部分解决方案的问题。如果答案是否定的，那么算法可以立即回溯，避免浪费时间，这使得它更容易显示任何两个完整解决方案之间的延迟保证。

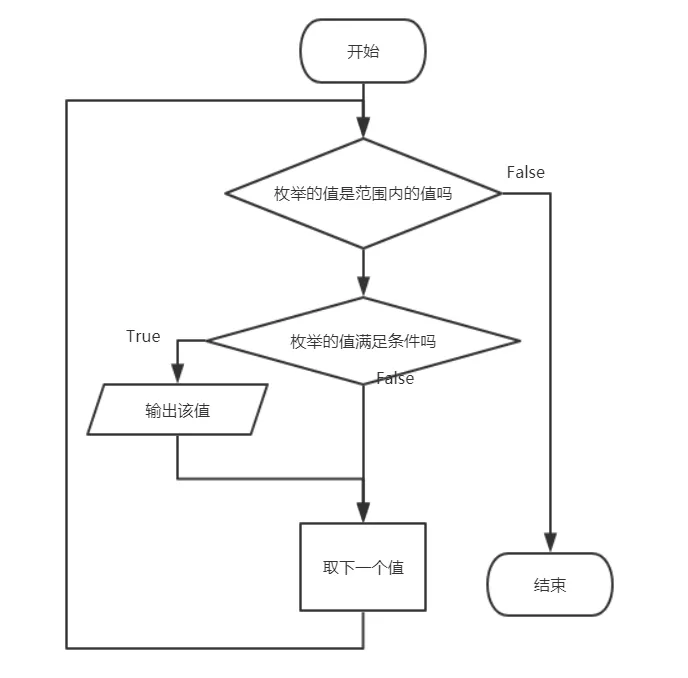
特别是，这种技术很适用于自还原问题。集合操作下的封闭。如果我们希望列举两个集合的不相交的联合，那么我们可以通过列举xxx个集合，然后列举第二个集合来解决问题。如果联合体不是不相交的，但是这两个集合可以按照排序的顺序进行枚举，那么可以在两个集合上并行地进行枚举，同时快速消除重复的集合。如果联合体不是不相交的，并且两个集合都没有被排序，那么可以以更高的内存使用率为代价来消除重复的部分，例如使用哈希表。同样，两个集合的笛卡尔乘积也可以通过列举一个集合并将每个结果与列举第二步时得到的所有结果连接起来来有效地列举。