最近的字符串
编辑在理论计算机科学中,最近的字符串是一个NP-hard计算问题,它试图找到一组输入字符串的几何中心。为了理解中心这个词,有必要在两个字符串之间定义一个距离。通常情况下,研究这个问题时要考虑到汉明距离。
正式定义
编辑更正式地说,给定n个长度为m的字符串s1,s2,…,sn,最接近的字符串问题寻求一个新的长度为m的字符串s,使d(s,si)≤k,对于所有i,其中d表示汉明距离,k是尽可能小。最接近字符串问题的决策问题版本是NP-complete的,它将k作为另一个输入,并询问是否有一个字符串在所有输入字符串的汉明距离k之内。最接近的字符串问题可以被看作是通用1中心问题的一个特例,其中元素之间的距离用汉明距离来衡量。
最近的字符串的动机
编辑在生物信息学中,最接近的字符串问题是寻找DNA中信号问题的一个深入研究的方面。
简化和数据减少
编辑最接近字符串的实例可能包含对问题不重要的信息。从某种意义上说,最接近字符串的通常输入包含的信息对问题的难易程度没有帮助。例如,如果一些字符串包含字符a,但没有包含字符z,那么用z替换所有的as,将产生一个基本等同的实例,也就是说:从修改后的实例的解决方案中,可以恢复原来的解决方案,反之亦然。
归一化输入
编辑当所有具有相同长度的输入字符串被写在彼此的上面时,它们就形成了一个矩阵。某些行的类型对解决方案的影响基本相同。例如,用另一列(x,x,y)替换有条目(a,a,b)的一列可能会导致不同的解串,但不能影响可解性,因为这两列表达了相同的结构,即前两个条目相等,但与第三条不同。一个输入实例可以被规范化,方法是在每一列中用a替换出现频率最高的字符,用b替换出现频率第二高的字符,依此类推。给出一个归一化实例的解决方案,通过将解决方案中的字符重新映射到每一列的原始版本,就可以找到原始实例。列的顺序对问题的难易程度没有帮助。也就是说,如果我们按照一定的排列组合π对所有的输入字符串进行排列组合,并得到该修改后的实例的解决方案字符串s,那么π-1(s)将是原始实例的解决方案。
最近的字符串的例子
编辑给出一个有三个输入字符串uvwx、xuwv和xvwu的实例。这可以写成这样的一个矩阵。第一列是数值(u,x,x)。由于x是出现频率最高的字符,我们用a代替它,我们用b代替u,即第二个出现频率最高的字符,得到新的第一列(b,a,a)。第二列的数值是(v,u,v)。与第一列一样,v被替换为a,u被替换为b,得到新的第二列(a,b,a)。对所有的列做同样的处理,就得到了规范化的实例
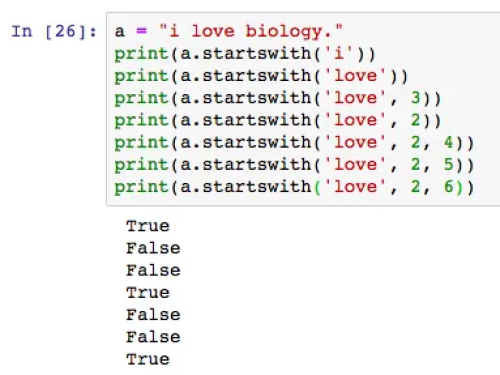
通过归一化得到的数据减少
编辑归一化输入将字母表的大小减少到最多是输入字符串的数量。这对那些运行时间取决于字母表大小的算法很有用。
近似性
编辑Li等人发展了一个多项式时间的近似方案,由于隐藏的常数很大,实际上是无法使用的。固定参数的可操作性最接近的字符串可以在以下时间内解决{dISPlaystyleO(kL+kdcdotd{d})},其中k是输入字符串的数量,L是所有字符串的长度,d是所有字符串的长度。其中,k是输入字符串的数量,L是所有字符串的长度,d是所需的从解决方案字符串到任何输入字符串的最大距离。
与其他问题的关系
编辑最接近字符串是更普遍的最接近子串问题的一个特例,严格来说,它更难。虽然最接近字符串在很多方面都是固定参数的,但最接近子串在这些参数方面是W[1]级难度。
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/163815/
