最长递增子序列

在计算机科学中，最长递增子序列问题是找到一个给定序列的子序列，其中子序列的元素按排序顺序，从低到高，并且子序列尽可能长。这个子序列不一定是连续的，也不一定是xxx的。最长递增子序列在与数学有关的各种学科中被研究，包括算法学、随机矩阵理论、表示理论和物理学。最长递增子序列问题可以在以下时间内得到解决{displaystylen}表示输入序列的长度。表示输入序列的长度。

在二进制VanderCorput序列的前16项中0,8,4,12,2,10,6,14,1,9,5,13,3,11,7,15一个最长的递增子序列是0,2,6,9,11,15.这个子序列的长度为6；输入序列没有7个成员的递增子序列。

最长递增子序列问题与最长公共子序列问题密切相关，后者有一个二次方时间的动态编程解：一个序列的最长递增子序列{displaystyle1,2,ldots,n,}这种方法可以使效率xxx提高。这种方法可以变得更有效率，导致时间界限的形式为O(nloglogn)。{displaystyleO(nloglogn).}。包容图中xxx的clique对应于定义该图的包容的最长递减子序列（假设原始非包容序列从最低值到最高值排序）。同样地，包络图中的xxx独立集对应于最长的非递减子序列。

因此，最长递增子序列算法可用于有效解决包络图中的悬崖问题。在包络图和杨氏表格之间的Robinson-Schensted对应关系中，对应于包络图的xxx行的长度等于包络图最长递增子序列的长度，xxx列的长度等于最长递减子序列的长度。

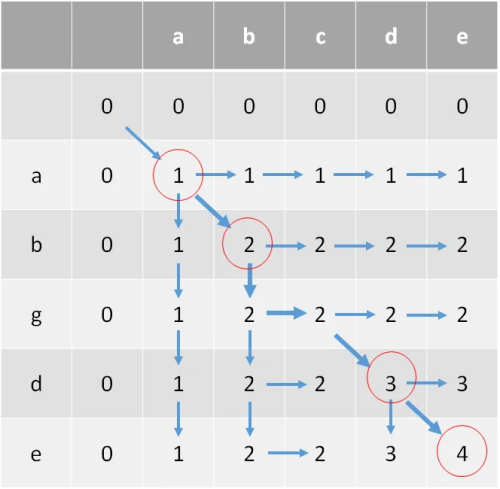
下面概述的算法用数组和二进制搜索有效地解决了最长递增子序列问题。它按顺序处理序列元素，保持迄今发现的最长递增子序列。将序列值表示为{displaystyleL}存储了迄今为止发现的最长的递增子序列的长度。-存储迄今为止发现的最长的递增子序列的长度。