蒙塔格语法

蒙塔格语法是一种自然语言语义学的方法，特别是高阶谓词逻辑和λ微积分，并通过克里普克模型，利用了扩展逻辑的概念。Montague在20世纪60年代和70年代初开创了这种方法。综上所述，蒙塔古的论点是，自然语言（如英语）和形式语言（如编程语言）可以用同样的方式对待。在我看来，自然语言和逻辑学家的人工语言之间没有重要的理论区别；事实上，我认为有可能在一个单一的自然和数学上的精确理论中理解这两种语言的语法和语义。在这一点上，我与一些哲学家不同，但我相信，我同意乔姆斯基和他的伙伴们的观点。语法中的句法类别的类型如下，其中t表示术语（对实体的指称），f表示公式。一个句子的意义由规则得到{displaystyleS:{mathit{NP}}{mathit{VP}}得到的句子的意义。｝是通过将NP的函数应用于VP的函数而得到的。VP和NP的类型可能会显得不直观，因为有一个问题，即一个不是简单术语的名词短语的意义。这是因为许多名词短语的意义，如吹口哨的人，在谓词逻辑中不仅仅是术语，还包括活动的谓词，如口哨，这不能在术语中表示（由常数和函数符号组成，但不是谓词）。所以我们需要一些术语。动词短语VP的含义可以用该术语来表达，比如说说明某个特定的x满足sleeps(x)∧{displaystyle{wedge}（显示方式）。snores(x)（表示为一个从x到该公式的函数）。现在，与NP相关的函数采用了那种函数，并将其与表达名词短语的意义所需的公式结合起来。这种陈述NP和VP的特殊方式并不是xxx可能的方式。关键是一个表达式的意义是作为其组成部分的函数获得的，要么是通过函数应用（用黑体括号包围函数和参数表示），要么是通过从与组成部分相关的函数中构造一个新函数。

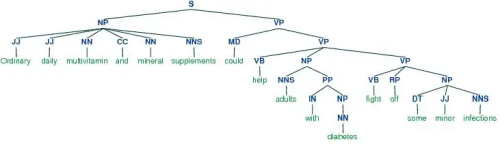
这种构成性使我们有可能为任意复杂的句子结构可靠地分配意义，包括辅助句和许多其他复杂情况。其他类别的表达的意义要么是类似的函数应用，要么是高阶函数。下面是语法的规则，xxx列表示一个非终端符号，第二列表示从其他非终端和终端产生该非终端的一种可能方式，第三列表示相应的意义。下面是根据上述语法的例子表达式及其相关的意义，表明一个给定的句子的意义是由其组成的表达式形成的，要么形成一个新的高阶函数，要么将一个表达式的高阶函数用于另一个表达式的意义。下面是其他一些被语法翻译成谓词逻辑的句子的例子。