图的同态性

在图论的数学领域，图的同态性是两个图之间尊重其结构的映射。更具体地说，它是两个图的顶点集之间的一个函数，将相邻的顶点映射到相邻的顶点。同态性概括了图着色的各种概念，并允许表达一类重要的约束满足问题，如某些调度或频率分配问题。同态可以组成的事实导致了丰富的代数结构：图上的前序、分布格和类别（一个用于无向图，一个用于有向图）。在给定的图之间寻找同态的计算复杂性一般来说是令人望而却步的，但有很多已知的特殊情况可在多项式时间内解决。可解决和不可解决的情况之间的界限一直是一个活跃的研究领域。

在本文中，除非另有说明，图是有限的无向图，允许有循环，但不允许有多条边（平行边）。图同构f从图G=（V（G），E（G））到图H=（V（H），E（H）），写作f:G→H形式上，{u,v}∈E(G)意味着{f(u),f(v)}∈E(H)，适用于V(G)中的所有顶点对u,v。如果存在任何从G到H的同态性，那么G被称为与H同态或H-可着色。这通常被表示为只是。G→H。上述定义可以扩展到有向图。那么，对于同构f:G→H，只要(u,v)是G的一个弧，(f(u),f(v))就是H的一个弧（有向边）。当且仅当G是H的一个子图时，存在一个从G到H的注入性同构（即一个从不将不同的顶点映射到一个顶点的同构）。如果同构f:G→H是一个双射（G和H的顶点之间的一对一对应），其反函数也是一个图同构，那么f就是一个图同构。覆盖图是一种特殊的同态，它反映了拓扑学中覆盖图的定义和许多特性。它们被定义为射影同态（即对每个顶点的东西映射），同时也是局部双射，即对每个顶点的邻域的双射。一个例子是双位数双覆盖，由图形成，将每个顶点v分成v0和v1，用边u0，v1和v0，u1替换每个边u，v。覆盖中的v0和v1映射到原图中的v的函数是一个同态性和覆盖图。图的同态性是一个不同的概念，与同态性没有直接关系。粗略地说，它需要注入性，但允许将边映射到路径上（而不仅仅是映射到边上）。图小数是一个更为宽松的概念。

如果G→H和H→G，那么两个图G和H是同态等价的，这些映射不一定是射影的，也不一定是注入的。例如，完整的二方图K2,2和K3,3是同态等价的：每个映射可以定义为取域图的左半部（或右半部），并映射到图像图的左半部（或右半部）中的一个顶点。缩减是指从图G到G的子图H的同态性r，使得对于H的每个顶点v来说，r(v)=v，在这种情况下，子图H称为G的缩减。核心图是一个与任何适当子图没有同构关系的图。等价地，核心可以被定义为不缩减到任何适当子图的图。每个图G都同态地等价于一个xxx的核心（直到同态），称为G的核心。

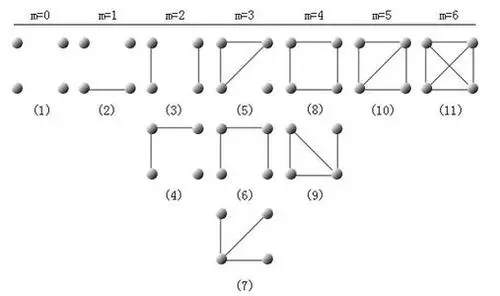
然而，同样的定义适用于有向图，有向图也等价于一个xxx的核心。每个图和每个有向图都包含其作为缩减和作为诱导子图的核心。例如，所有完整图Kn和所有奇数周期（奇数长度的周期图）都是核心。每个包含三角形的3色图G（即有完整图K3作为子图）都与K3同构。这是因为，一方面，G的3色与G→K3的同构是一样的，如下文所解释。另一方面，G的每一个子图都有一个进入G的同态性，这意味着K3→G，这也意味着K3是任何此类图G的核心。

对于某个整数k，k着色是指对图G的每个顶点分配k种颜色中的一种，从而使每条边的端点得到不同颜色。G的k-着色正好对应于从G到完整图Kk的同态性。事实上，Kk的顶点对应于k种颜色，当且仅当两种颜色不同时，它们作为Kk的顶点是相邻的。因此，当且仅当一个函数将G的相邻顶点映射到Kk时，它定义了一个与Kk的同构。